Question

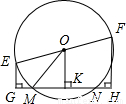
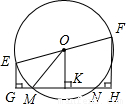
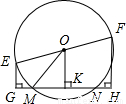
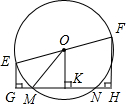如图，EF是圆O的直径，OE=5cm，弦MN=8cm，则E，F两点到直线MN距离的和等于（　　）

• A、12cm
• B、6cm
• C、8cm
• D、3cm

Answer 1

分析：由图可以明显的看出OK∥EG∥FH，而O是EF的中点，因此OK是梯形EGHF的中位线，欲求EG+FH的值，需求出OK的长；在Rt△OMK中，由垂径定理易知MK的长度，即可根据勾股定理求出OK的值，由此得解．

解答：解：∵EG⊥GH，OK⊥GH，FH⊥GH，
∴EG∥OK∥FH；
∵EO=OF，
∴OK是梯形EGHF的中位线，即EG+FH=2OK；
Rt△OKM中，MK=

1

2

MN=4cm，OM=OE=5cm；
由勾股定理，得：OK=

OM2-MK2

=3cm；
∴EG+FH=2OK=6cm．
故选B．

点评：此题主要考查了垂径定理、勾股定理以及梯形中位线定理的综合应用．