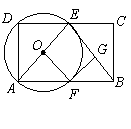
题目内容
如图 ,矩形![]() 中,
中,![]() .点
.点![]() 是
是![]() 上的动点,以
上的动点,以![]() 为直径的
为直径的![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
(1)当![]() 是
是![]() 的中点时:
的中点时:
①![]() 的值为______________;
的值为______________;
② 证明:![]() 是
是![]() 的切线;
的切线;
(2)试探究:![]() 能否与
能否与![]() 相切?若能,求出此时
相切?若能,求出此时![]() 的长;若不能,请说明理由.
的长;若不能,请说明理由.

(1)①![]()
②法一:在矩形![]() 中,
中,![]() ,
,
![]() ,又
,又![]() ,
,
∴![]() ,
,
得![]() ,
,
连![]() ,则
,则![]() , ∴
, ∴![]() ,
,
![]() , ∴
, ∴![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
∴![]() 是
是![]() 的切线
的切线
 |
(2)法一:若![]() 能与
能与![]() 相切, ∵
相切, ∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,则
,则![]() ,
,
又![]() , ∴
, ∴![]() ,
,
∴![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]() ,得
,得![]() ,
,
整理得![]() .
.
∵![]() , ∴该方程无实数根.
, ∴该方程无实数根.
∴点![]() 不存在,
不存在,![]() 不能与
不能与![]() 相切.
相切.
法二: 若![]() 能与
能与![]() 相切,因
相切,因![]() 是
是![]() 的直径,则
的直径,则![]() ,
,
设![]() ,则
,则![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
即![]() , 整理得
, 整理得![]() ,
,
∵![]() , ∴该方程无实数根.
, ∴该方程无实数根.
∴点![]() 不存在,
不存在,![]() 不能与
不能与![]() 相切.
相切.
(法三:本题可以通过判断以![]() 为直径的圆与
为直径的圆与![]() 是否有交点来求解,参照前一解法给分)
是否有交点来求解,参照前一解法给分)

练习册系列答案
相关题目
 中,
中,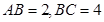 ,点
,点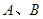 分别在
分别在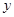 轴、
轴、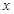 轴的正半轴上,点
轴的正半轴上,点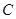 在第一象限,如果
在第一象限,如果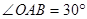 ,那么点
,那么点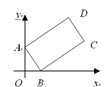
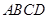 中,点
中,点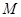 在
在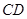 边上,连接
边上,连接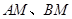 ,
,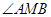
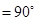 ,则点
,则点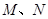 分别为矩形
分别为矩形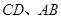 上的直角点,且
上的直角点,且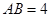 ,
,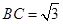 ,则
,则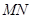 的长为
的长为 
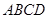 中,
中,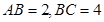 ,点
,点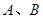 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点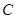 在第一象限,如果
在第一象限,如果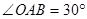 ,那么点
,那么点