题目内容
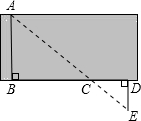
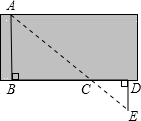如图，要测量河宽，可在两岸找到相对的两点A、B，先从B出发与AB成90°方向向前走50米，到C处立一标杆，然后方向不变继续朝前走10米到D处，在D处转90°，沿DE方向走到E处，若A、C、E三点恰好在同一直线上，且DE=17米，你能根据题目提供的数据和图形求出河宽吗？
解：∵先从B处出发与AB成90°角方向，
∴∠ABC=90°，
∵BC=50m，CD=10m，∠EDC=90°，
∴△ABC∽△EDC，
∴AB=5DE，
∵沿DE方向再走17米，到达E处，即DE=17，
∴AB=5×17=85．
∴河宽为85米．
分析：根据已知条件求证△ABC≌△EDC，利用其对应边相等的性质即可求得AB．
点评：本题考查了相似三角形对应边相等的性质，考查了全等三角形的判定，难度不大，属于基础题．
∴∠ABC=90°，
∵BC=50m，CD=10m，∠EDC=90°，
∴△ABC∽△EDC，
∴AB=5DE，
∵沿DE方向再走17米，到达E处，即DE=17，
∴AB=5×17=85．
∴河宽为85米．
分析：根据已知条件求证△ABC≌△EDC，利用其对应边相等的性质即可求得AB．
点评：本题考查了相似三角形对应边相等的性质，考查了全等三角形的判定，难度不大，属于基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
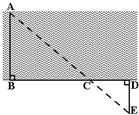27、如图，要测量河宽，可在两岸找到相对的两点A、B，先从B出发与AB成90°方向向前走50米，到C处立一标杆，然后方向不变继续朝前走10米到D处，在D处转90°，沿DE方向走到E处，若A、C、E三点恰好在同一直线上，且DE=17米，你能根据题目提供的数据和图形求出河宽吗？