题目内容
 平面直角坐标系中,直线y=-x+5交x轴、y轴于A、B两点,C(2,m)是直线AB上一点,过点C的直线交x轴于点D(-2,0)
平面直角坐标系中,直线y=-x+5交x轴、y轴于A、B两点,C(2,m)是直线AB上一点,过点C的直线交x轴于点D(-2,0)(1)求直线CD的函数解析式;
(2)已知直线CD交y轴于点E,求△BCE的面积;
(3)设P是折线段D-A-B上的一动点(异于点D、C),若△PCD是直角三角形,求PD的长.
考点:一次函数综合题
专题:
分析:(1)利用待定系数法求一次函数解析式得出即可;
(2)过C点作CF垂直于BE交y轴于F,利用三角形面积求法得出BE,CF的长即可得出答案;
(3)利用C点、D点不可能是直角三角形的顶点,则只有可能是P点是直角顶点,过C点作CM垂直于AD于M,过D点作DN垂直于AB于N,当P点与M点重合时,当P点与N点重合时,分别求出即可.
(2)过C点作CF垂直于BE交y轴于F,利用三角形面积求法得出BE,CF的长即可得出答案;
(3)利用C点、D点不可能是直角三角形的顶点,则只有可能是P点是直角顶点,过C点作CM垂直于AD于M,过D点作DN垂直于AB于N,当P点与M点重合时,当P点与N点重合时,分别求出即可.
解答: 解:(1)∵C在y=-x+5上,令x=2,则y=-2+5=3,
解:(1)∵C在y=-x+5上,令x=2,则y=-2+5=3,
得m=3,所以C(2,3),
设CD解析式为y=kx+b把点C(2,3)、D(-2,0)代入y=kx+b得
,
解得:
,
所以直线CD的函数解析式为:y=
x+
;
(2)如图,过C点作CF垂直于BE交y轴于F,
因为直线CD交y轴于点E,所以令直线CD的x=0,得y=1.5,
所以E(0,1.5)所以S△BCE=
•BE•CF=
×(5-1.5)×2=3.5;
(3)如图,∵C点、D点不可能是直角三角形的顶点,∴只有可能是P点是直角顶点,
∴过C点作CM垂直于AD于M,过D点作DN垂直于AB于N,
当P点与M点重合时,DP=DM=OD+OM=4;
当P点与N点重合时,∵∠BAD=45°,
∴∠NDA=45°,
则直线DN垂直于直线AB,
又∵直线DN过D(-2,0),
所以直线DN的表达式为:y=x+2.
直线AB:y=-x+5与直线DN:y=x+2联立方程组,得:
,
解得:
所以N(1.5,3.5),
所以DP′=DN=
=
,
综上所述:若△PCD是直角三角形,PD的长为4或
.
 解:(1)∵C在y=-x+5上,令x=2,则y=-2+5=3,
解:(1)∵C在y=-x+5上,令x=2,则y=-2+5=3,得m=3,所以C(2,3),
设CD解析式为y=kx+b把点C(2,3)、D(-2,0)代入y=kx+b得
|
解得:
|
所以直线CD的函数解析式为:y=
| 3 |
| 4 |
| 3 |
| 2 |
(2)如图,过C点作CF垂直于BE交y轴于F,
因为直线CD交y轴于点E,所以令直线CD的x=0,得y=1.5,
所以E(0,1.5)所以S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图,∵C点、D点不可能是直角三角形的顶点,∴只有可能是P点是直角顶点,
∴过C点作CM垂直于AD于M,过D点作DN垂直于AB于N,
当P点与M点重合时,DP=DM=OD+OM=4;
当P点与N点重合时,∵∠BAD=45°,
∴∠NDA=45°,
则直线DN垂直于直线AB,
又∵直线DN过D(-2,0),
所以直线DN的表达式为:y=x+2.
直线AB:y=-x+5与直线DN:y=x+2联立方程组,得:
|
解得:
|
所以N(1.5,3.5),
所以DP′=DN=
(
|
| 7 |
| 2 |
| 2 |
综上所述:若△PCD是直角三角形,PD的长为4或
| 7 |
| 2 |
| 2 |
点评:此题主要考查了一次函数综合以及二元一次方程解法和三角形面积求法等知识,利用分类讨论得出是解题关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
下列运算正确的是( )
| A、2a+3b=5ab |
| B、2(2a-b)=4a-b |
| C、a-(a-b)=-b |
| D、-2(a-1)+2a=2 |
若x-3y=-3,则5-2x+6y的值是( )
| A、-1 | B、2 | C、8 | D、11 |
 如图,点A、B、C都在⊙O上,若∠A=44°,则∠BOC的度数为( )
如图,点A、B、C都在⊙O上,若∠A=44°,则∠BOC的度数为( )| A、22° | B、44° |
| C、46° | D、88° |
 如图,将一副直角三角板叠放在一起,使直角顶点重合于点C,若∠ACD=120°,则
如图,将一副直角三角板叠放在一起,使直角顶点重合于点C,若∠ACD=120°,则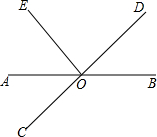 如图,直线AB、CD相交于点O,OA平分∠COE,∠DOB=40°.求∠DOE.
如图,直线AB、CD相交于点O,OA平分∠COE,∠DOB=40°.求∠DOE. 如图,在Rt△ABC中,a=5,c=13,求sinA,cosA,tanA.
如图,在Rt△ABC中,a=5,c=13,求sinA,cosA,tanA.