题目内容
 如图,AB是⊙O的直径,AC、AD分别是⊙O的弦,且AC平分∠BAD,过点C作CE⊥AD交AD延长线于点E.
如图,AB是⊙O的直径,AC、AD分别是⊙O的弦,且AC平分∠BAD,过点C作CE⊥AD交AD延长线于点E.(1)求证:CE是⊙O的切线;
(2)若DE=1,AD=2,试解答下列问题:
①求AC的长;
②求弦AC、AD与劣弧CD所围成图形的面积.
分析:(1)连接OC,则可得OC=OA,∠OAC=∠OCA,再结合AC平分∠BAD,可判断OC∥AE,继而可判断出结论.
(2)①根据切线的性质得出∠ECD=∠EAC,从而可判断出△CED∽△AEC,利用相似三角形的性质求出CE的长度,在RT△ACE中,利用勾股定理可求出AC的长度.
②在RT△ACE中,利用三角函数的知识,可求出∠CAE的度数,继而可判断出DC∥AB,△OAD、△OCD是等边三角形,可将弦AC、AD与劣弧CD所围成图形的面积,转化为扇形OCD的面积,代入扇形面积公式进行计算即可.
(2)①根据切线的性质得出∠ECD=∠EAC,从而可判断出△CED∽△AEC,利用相似三角形的性质求出CE的长度,在RT△ACE中,利用勾股定理可求出AC的长度.
②在RT△ACE中,利用三角函数的知识,可求出∠CAE的度数,继而可判断出DC∥AB,△OAD、△OCD是等边三角形,可将弦AC、AD与劣弧CD所围成图形的面积,转化为扇形OCD的面积,代入扇形面积公式进行计算即可.
解答: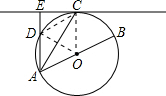 解:(1)连接OC,OD,
解:(1)连接OC,OD,
∵OC=OA,
∴∠OAC=∠OCA,
又∵AC平分∠BAD,
∴∠CAD=∠CAO=∠OCA,
∴OC∥AE,即可得OC⊥CE,
故可得CE是⊙O的切线;
(2)①∵CE是⊙O的切线,
∴∠ECD=∠EAC,
∴△CED∽△AEC,
则
=
,即CE2=AE•DE=3,
解得:CE=
,
在RT△AEC中,AC=
=
=2
.
②由①的结论,可得tan∠CAE=
=
,
故∠CAE=30°,
∵∠OCA=∠OAC=∠CAE,
∴∠ACD=90°-∠ACE-∠ACO=30°,
故可得∠ACD=∠CAO,△AOD、△COD均是等边三角形,
则⊙O的半径R=AD=2,
故DC∥AB,则△ADC的面积与△COD的面积相等,
从而可得弦AC、AD与劣弧CD所围成图形的面积与扇形OCD的面积相等,
则S扇形OCD=
=
.
即弦AC、AD与劣弧CD所围成图形的面积为
.
 解:(1)连接OC,OD,
解:(1)连接OC,OD,∵OC=OA,
∴∠OAC=∠OCA,
又∵AC平分∠BAD,
∴∠CAD=∠CAO=∠OCA,
∴OC∥AE,即可得OC⊥CE,
故可得CE是⊙O的切线;
(2)①∵CE是⊙O的切线,
∴∠ECD=∠EAC,
∴△CED∽△AEC,
则
| CE |
| AE |
| DE |
| CE |
解得:CE=
| 3 |
在RT△AEC中,AC=
| EC2+AE2 |
| 3+9 |
| 3 |
②由①的结论,可得tan∠CAE=
| CE |
| AE |
| ||
| 3 |
故∠CAE=30°,
∵∠OCA=∠OAC=∠CAE,
∴∠ACD=90°-∠ACE-∠ACO=30°,
故可得∠ACD=∠CAO,△AOD、△COD均是等边三角形,
则⊙O的半径R=AD=2,
故DC∥AB,则△ADC的面积与△COD的面积相等,
从而可得弦AC、AD与劣弧CD所围成图形的面积与扇形OCD的面积相等,
则S扇形OCD=
| 60πR2 |
| 360 |
| 2π |
| 3 |
即弦AC、AD与劣弧CD所围成图形的面积为
| 2π |
| 3 |
点评:此题属于圆的综合性题目,涉及了切线的判定与性质、勾股定理,三角函数值及相似三角形的判定与性质,解答本题的关键是利用相似三角形的性质求出AC的长度,然后判断出DC∥AB,将所求不规则面积转化为扇形的面积,难度较大.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为