题目内容
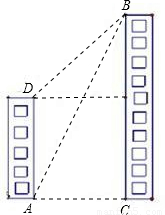
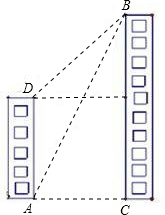 如图:小虎家住在高80米的公寓AD内,他家的河对岸新修了一座大厦的高度,小虎在他家的楼底A测得大厦顶部B的仰角为60°,爬到楼顶D处测得大厦顶部B的仰角为30度.请根据小虎计算出大厦的高BC.
如图:小虎家住在高80米的公寓AD内,他家的河对岸新修了一座大厦的高度,小虎在他家的楼底A测得大厦顶部B的仰角为60°,爬到楼顶D处测得大厦顶部B的仰角为30度.请根据小虎计算出大厦的高BC.
分析:首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形Rt△ABC、Rt△BDE,应利用其公共边AC构造等量关系,借助BC-BE=AD=80构造方程关系式,进而可求AC的值,再求出BC的答案.
解答:解:设AC=x,过点D作DE⊥BC于点E;
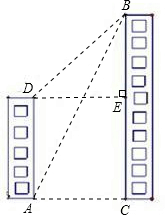
根据题意:在Rt△ABC中,有BC=AC×tan60°=
x,
在Rt△BDE中,有BE=AC×tan30°=
x,
且BC-BE=AD=80;即(
x-
x)=80,
解可得:x=40
;则BC=AC×tan60°=
x=120米.
答:大厦的高BC为120米.

根据题意:在Rt△ABC中,有BC=AC×tan60°=
| 3 |
在Rt△BDE中,有BE=AC×tan30°=
| ||
| 3 |
且BC-BE=AD=80;即(
| 3 |
| ||
| 3 |
解可得:x=40
| 3 |
| 3 |
答:大厦的高BC为120米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 如图:小虎家住在高80米的公寓AD内,他家的河对岸新修了一座大厦的高度,小虎在他家的楼底A测得大厦顶部B的仰角为60°,爬到楼顶D处测得大厦顶部B的仰角为30度.请根据小虎计算出大厦的高BC.
如图:小虎家住在高80米的公寓AD内,他家的河对岸新修了一座大厦的高度,小虎在他家的楼底A测得大厦顶部B的仰角为60°,爬到楼顶D处测得大厦顶部B的仰角为30度.请根据小虎计算出大厦的高BC.