题目内容
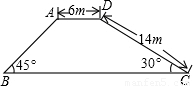
 如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m).(参考数据:
如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m).(参考数据:| 2 |
| 3 |
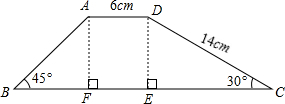
分析:在Rt△ABF中求出BF,在Rt△CDE中求出DE、EC,从而可得出坝高和坝底宽.
解答:解:如图,作DE垂直BC于点E,AF垂直BC于点F,
 在Rt△DEC中,∵CD=14m,∠DCE=30°,
在Rt△DEC中,∵CD=14m,∠DCE=30°,
∴DE=DC•sin30°=14×
=7(m),
∴EC=DC•cos30°=14×
=7
(m),
由梯形性质,得AF=DE=7m,EF=AD=6m,
Rt△AFB中,∵∠ABF=45°,
∴BF=AF=7m,
∴BC=BF+EF+CE=7+6+7
=13+7
=13+7×1.73≈25.1(m).
答:坝高为7m,坝底约为25.1m.
 在Rt△DEC中,∵CD=14m,∠DCE=30°,
在Rt△DEC中,∵CD=14m,∠DCE=30°,∴DE=DC•sin30°=14×
| 1 |
| 2 |
∴EC=DC•cos30°=14×
| ||
| 2 |
| 3 |
由梯形性质,得AF=DE=7m,EF=AD=6m,
Rt△AFB中,∵∠ABF=45°,
∴BF=AF=7m,
∴BC=BF+EF+CE=7+6+7
| 3 |
| 3 |
答:坝高为7m,坝底约为25.1m.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用解直角三角形的知识得出有关线段的长度,难度一般.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
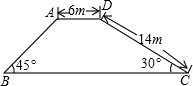 如图,一座堤坝的横截面是梯形,根据图中给出的数据,则坝底宽BC为( )(精确到0.1m,参加数据:
如图,一座堤坝的横截面是梯形,根据图中给出的数据,则坝底宽BC为( )(精确到0.1m,参加数据:| 2 |
| 3 |
| A、20m | B、22.9m |
| C、24m | D、25.1m |
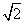 =1.414,
=1.414,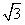 =1.732
=1.732 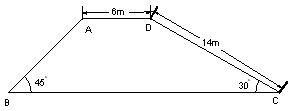
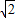 =1.414,
=1.414,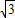 =1.732.
=1.732.