题目内容
如图， |
| BC |
|
| CD |
|
| DE |
分析：由
=
=
，∠BOC=40°，根据等弧所对的圆周角相等，可求得∠EOD与∠COD的度数，继而求得答案．
|
| BC |
|
| CD |
|
| DE |
解答：解：∵
=
=
，∠BOC=40°，
∴∠EOD=∠COD=∠BOC=40°，
∵AB是⊙O的直径，
∴∠AOE=180°-∠EOD-∠COD-∠BOC=60°．
故选B．
|
| BC |
|
| CD |
|
| DE |
∴∠EOD=∠COD=∠BOC=40°，
∵AB是⊙O的直径，
∴∠AOE=180°-∠EOD-∠COD-∠BOC=60°．
故选B．
点评：此题考查了弧与圆心角的关系．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
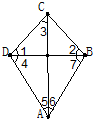27、如图，BC⊥CD，∠1=∠2=∠3，∠4=60°，∠5=∠6．
24、如图，BC⊥CD，∠1=∠2=∠3，∠4=60°，∠5=∠6．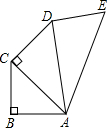
如图AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则AE等于
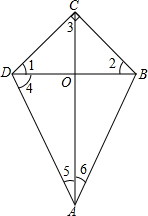如图，BC⊥CD，∠1=∠2=∠3，∠4=70°，∠5=∠6