题目内容
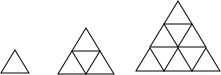
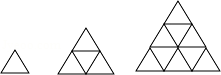
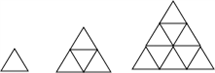
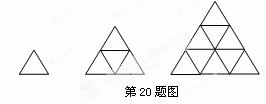
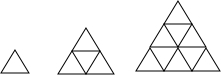 如图,用火柴摆上系列图案,按这种方式摆下去,当每边摆10根时(即n=10)时,需要的火柴棒总数为( )根.
如图,用火柴摆上系列图案,按这种方式摆下去,当每边摆10根时(即n=10)时,需要的火柴棒总数为( )根.| A、165 | B、65 | C、110 | D、55 |
分析:图形从上到下可以分成几行,第n行中,斜放的火柴有2n根,下面横放的有n根,因而图形中有n排三角形时,火柴的根数是:斜放的是2+4+…+2n=2(1+2+…+n),横放的是:1+2+3+…+n,则每排放n根时总计有火柴数是:3(1+2+…+n)=
.把n=10代入就可以求出.
| 3n(n+1) |
| 2 |
解答:解:根据题意得出规律每排放n根时总计有火柴数是:3(1+2+…+n)=
,
当每边摆10根(即n=10)时,需要的火柴棒总数为
=165.
故选A.
| 3n(n+1) |
| 2 |
当每边摆10根(即n=10)时,需要的火柴棒总数为
| 3×10(10+1) |
| 2 |
故选A.
点评:观察图形总结出规律是解决本题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目