题目内容
已知等腰三角形的底边和一腰长是方程组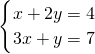
的解，求这个三角形的各边长．
解：
，
由①得，x=4-2y③，
③代入②得，3（4-2y）+y=7，
解得y=1，
把y=1代入③得，x=4-2×1=2，
所以，方程组的解是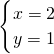
，
当2是腰长时，三角形的三边分别为2、2、1，
能组成三角形，
当1是腰时，三角形的三边分别为1、1、2，
∵1+1=2，
∴不能组成三角形，
综上所述，三角形的三边分别为2、2、1．
分析：先把第一个方程整理成x=4-2y，然后利用代入消元法求解，再根据等腰三角形的两腰相等讨论求解即可．
点评：本题考查的是二元一次方程组的解法，方程组中未知数的系数较小时可用代入法，当未知数的系数相等或互为相反数时用加减消元法较简单．
，由①得，x=4-2y③，
③代入②得，3（4-2y）+y=7，
解得y=1，
把y=1代入③得，x=4-2×1=2，
所以，方程组的解是
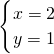，当2是腰长时，三角形的三边分别为2、2、1，
能组成三角形，
当1是腰时，三角形的三边分别为1、1、2，
∵1+1=2，
∴不能组成三角形，
综上所述，三角形的三边分别为2、2、1．
分析：先把第一个方程整理成x=4-2y，然后利用代入消元法求解，再根据等腰三角形的两腰相等讨论求解即可．
点评：本题考查的是二元一次方程组的解法，方程组中未知数的系数较小时可用代入法，当未知数的系数相等或互为相反数时用加减消元法较简单．
练习册系列答案
相关题目