题目内容
 (2012•南充)在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
(2012•南充)在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.(1)求证:MA=MB;
(2)连接AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
分析:(1)过点M作ME⊥OP于点E,作MF⊥OQ于点F,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得∠AME=∠BMF,再利用“角边角”证明△AME和△BMF全等,根据全等三角形对应边相等即可证明;
(2)根据全等三角形对应边相等可得AE=BF,设OA=x,表示出AE为2-x,即BF的长度,然后表示出OB=2+(2-x),再利用勾股定理列式求出AM,然后根据等腰直角三角形的斜边等于直角边的
倍表示出AB的长度,然后根据三角形的周长公式列式判断出△AOB的周长随AB的变化而变化,再根据二次函数的最值问题求出周长最小时的x的值,然后解答即可.
(2)根据全等三角形对应边相等可得AE=BF,设OA=x,表示出AE为2-x,即BF的长度,然后表示出OB=2+(2-x),再利用勾股定理列式求出AM,然后根据等腰直角三角形的斜边等于直角边的
| 2 |
解答:(1)证明:如图,过点M作ME⊥OP于点E,作MF⊥OQ于点F,
∵∠O=90°,
∴四边形OEMF是矩形,
∵M是PQ的中点,OP=OQ=4,∠O=90°,
∴ME=
OQ=2,MF=
OP=2,
∴ME=MF,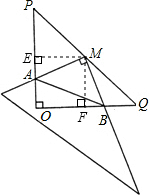
∴四边形OEMF是正方形,
∵∠AME+∠AMF=90°,∠BMF+∠AMF=90°,
∴∠AME=∠BMF,
在△AME和△BMF中,
,
∴△AME≌△BMF(ASA),
∴MA=MB;
(2)解:有最小值,最小值为4+2
.
理由如下:根据(1)△AME≌△BMF,
∴AE=BF,
设OA=x,则AE=2-x,
∴OB=OF+BF=2+(2-x)=4-x,
在Rt△AME中,AM=
=
,
∵∠AMB=90°,MA=MB,
∴AB=
AM=
•
=
,
△AOB的周长=OA+OB+AB=x+(4-x)+
=4+
,
所以,当x=2,即点A为OP的中点时,△AOB的周长有最小值,最小值为4+
,
即4+2
.
∵∠O=90°,
∴四边形OEMF是矩形,
∵M是PQ的中点,OP=OQ=4,∠O=90°,
∴ME=
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=MF,

∴四边形OEMF是正方形,
∵∠AME+∠AMF=90°,∠BMF+∠AMF=90°,
∴∠AME=∠BMF,
在△AME和△BMF中,
|
∴△AME≌△BMF(ASA),
∴MA=MB;
(2)解:有最小值,最小值为4+2
| 2 |
理由如下:根据(1)△AME≌△BMF,
∴AE=BF,
设OA=x,则AE=2-x,
∴OB=OF+BF=2+(2-x)=4-x,
在Rt△AME中,AM=
| AE2+ME2 |
| (2-x)2+22 |
∵∠AMB=90°,MA=MB,
∴AB=
| 2 |
| 2 |
| (2-x)2+22 |
| 2(2-x)2+8 |
△AOB的周长=OA+OB+AB=x+(4-x)+
| 2(2-x)2+8 |
| 2(2-x)2+8 |
所以,当x=2,即点A为OP的中点时,△AOB的周长有最小值,最小值为4+
| 8 |
即4+2
| 2 |
点评:本题考查了全等三角形的判定与性质,等腰直角三角的性质,三角形的中位线定理,勾股定理的应用,以及二次函数的最值问题,作出辅助线,把动点问题转化为固定的三角形,构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 (2012•南充)如图,把一个圆形转盘按1:2:3:4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为
(2012•南充)如图,把一个圆形转盘按1:2:3:4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为