题目内容
16、我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.若四边形ABCD中AC=BD,则四边形ABCD的中点四边形是
菱形
.分析:根据菱形的性质来解答该题.菱形的四条边相等,四边形的对角线就一定要相等故可以得到四边形的四条边相等,从而利用菱形的定义判定菱形.
解答:解: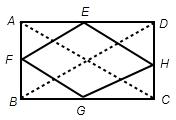
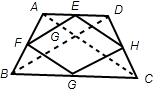
∵AC=BD,因为EFGH为菱形,则EH=EF.
∵E、F、G、H为四边中点,
∴AC=2EH=2FG,BD=2FE=2GH,
∵AC=BD,
∴EF=FG=GH=HE.
∴四边形EFGH为菱形,
故答案为菱形.


∵AC=BD,因为EFGH为菱形,则EH=EF.
∵E、F、G、H为四边中点,
∴AC=2EH=2FG,BD=2FE=2GH,
∵AC=BD,
∴EF=FG=GH=HE.
∴四边形EFGH为菱形,
故答案为菱形.
点评:本题考查了菱形的判定及三角形的中位线定理,根据三角形中位线定理和菱形四条边相等,求出四边形对角线相等.

练习册系列答案
相关题目