题目内容
本题分为A、B 两类题,你可从A、B 两类题中任选一题解答即可
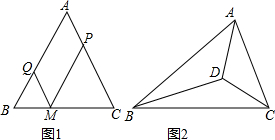
(A类):如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
(1)求四边形AQMP的周长;
(2)写出图中的两对相似三角形(不需证明);
(3)M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.
(B类):有人这样证明三角形内角和是180°,如图,D是△ABC内一点,连接AD、BD、CD,他们将△ABC分成了三个小的三角形.因此有:三个小三角形的内角和的和比△ABC的内角和多360°,如果设三角形内角 和是x,则有:x+x+x=x+360°,易解得x=180°,你认为这个证明正确吗?说说你的理由.
和是x,则有:x+x+x=x+360°,易解得x=180°,你认为这个证明正确吗?说说你的理由.
解:(1)∵AB=AC=a,
∴∠B=∠C,
又∵PM∥AB,QM∥AC,
∴∠PMC=∠B=∠C,∠QMB=∠C=∠B,
∴QM=QB,PM=PC,
∴四边形AQMP的周长为:AQ+QM+PM+AP
=AQ+QB+PC+AP
=AB+AC
=2a;
(2)由已知得:△QMB∽△ABC,△PMC∽△ABC;
(3)已知AB=AC,PM∥AB,QM∥AC,M位于BC的中点,
∴PM=QM= AB=
AB= AC,
AC,
∴AQ=PM=QM=AP,
∴四边形AQMP为菱形.
分析:A类(1)由已知AB=AC和PM∥AB,QM∥AC,可推出∠PMC=∠B=∠C,∠QMB=∠C=∠B,所以得QM=QB,PM=PC,从而求出四边形AQMP的周长;
(2)由PM∥AB,QM∥AC,可推出△QMB∽△ABC,△PMC∽△ABC;
(3)当M位于BC的中点时,由已知得PM=QM= AB=
AB= AC,所以四边形AQMP为菱形.
AC,所以四边形AQMP为菱形.
点评:此题考查的知识点是相似三角形、等腰三角形的性质及菱形的判定,解答此题的关键是运用等腰三角形的性质.
∴∠B=∠C,
又∵PM∥AB,QM∥AC,
∴∠PMC=∠B=∠C,∠QMB=∠C=∠B,
∴QM=QB,PM=PC,
∴四边形AQMP的周长为:AQ+QM+PM+AP
=AQ+QB+PC+AP
=AB+AC
=2a;
(2)由已知得:△QMB∽△ABC,△PMC∽△ABC;
(3)已知AB=AC,PM∥AB,QM∥AC,M位于BC的中点,
∴PM=QM=
 AB=
AB= AC,
AC,∴AQ=PM=QM=AP,
∴四边形AQMP为菱形.
分析:A类(1)由已知AB=AC和PM∥AB,QM∥AC,可推出∠PMC=∠B=∠C,∠QMB=∠C=∠B,所以得QM=QB,PM=PC,从而求出四边形AQMP的周长;
(2)由PM∥AB,QM∥AC,可推出△QMB∽△ABC,△PMC∽△ABC;
(3)当M位于BC的中点时,由已知得PM=QM=
 AB=
AB= AC,所以四边形AQMP为菱形.
AC,所以四边形AQMP为菱形.点评:此题考查的知识点是相似三角形、等腰三角形的性质及菱形的判定,解答此题的关键是运用等腰三角形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和是x,则有:x+x+x=x+360°,易解得x=180°,你认为这个证明正确吗?说说你的理由.
和是x,则有:x+x+x=x+360°,易解得x=180°,你认为这个证明正确吗?说说你的理由.