题目内容
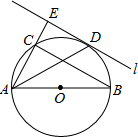 (2006•寿光市模拟)如图:已知△ABC内接于⊙O,AB是直径,∠BAC的平分线交⊙O于点D,过点D作⊙O的切线l,交AC边的延长线于点E,请写出三个正确结论①
(2006•寿光市模拟)如图:已知△ABC内接于⊙O,AB是直径,∠BAC的平分线交⊙O于点D,过点D作⊙O的切线l,交AC边的延长线于点E,请写出三个正确结论①∠ACB=90°
∠ACB=90°
②AC2+BC2=AB2
AC2+BC2=AB2
③∠EAD=∠BAD
∠EAD=∠BAD
(结论中的角、线段必须是图中现有的)分析:本题可以从圆周角定理、切线的性质定理、切线的判定定理、勾股定理以及角平分线的定义等出发填空即可,注意答案结论不唯一.
解答:解:∵AB是直径,
∴∠ACB=90°,
∴AC2+BC2=AB2,
∵∠BAC的平分线交⊙O于点D,
∴∠EAD=∠BAD,
∴∠ACB=90°,AC2+BC2=AB2,∠EAD=∠BAD,都成立.
故答案为:∠ACB=90°,AC2+BC2=AB2,∠EAD=∠BAD.
∴∠ACB=90°,
∴AC2+BC2=AB2,
∵∠BAC的平分线交⊙O于点D,
∴∠EAD=∠BAD,
∴∠ACB=90°,AC2+BC2=AB2,∠EAD=∠BAD,都成立.
故答案为:∠ACB=90°,AC2+BC2=AB2,∠EAD=∠BAD.
点评:本题考查了圆周角定理、切线的性质定理、切线的判定定理、勾股定理以及角平分线的定义,属于结论开放性题目.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (2006•寿光市模拟)将如图所示圆锥侧面展开恰为半圆,则锥角∠P的度数是( )
(2006•寿光市模拟)将如图所示圆锥侧面展开恰为半圆,则锥角∠P的度数是( )