题目内容
【题目】直线![]() 的解析式为
的解析式为![]() ,分别交
,分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() .
.
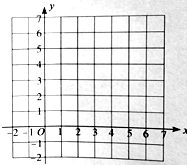
⑴写出![]() 两点的坐标,并画出直线
两点的坐标,并画出直线![]() 的图象;
的图象;
⑵将直线![]() 向上平移
向上平移![]() 个单位得到
个单位得到![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .作出
.作出![]() 的图象,
的图象,![]() 的解析式是 .
的解析式是 .
⑶将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,
,![]() 交
交![]() 于点
于点![]() .作出
.作出![]() 的图象,
的图象,![]() .
.
【答案】(1)A(1,0),B(0,2),图象见解析;(2)y=﹣2x+6;(3)![]() .
.
【解析】
试题分析:(1)分别令x=0求得y、令y=0求得x,即可得出A、B的坐标,从而得出直线l的解析式;
(2)将直线向上平移4个单位可得直线l1,根据“上加下减”的原则求解即可得出其解析式;
(3)由旋转得出其函数图象及点B的对应点坐标,待定系数法求得直线l2的解析式,继而求得其与y轴的交点,根据tan∠CAD=tan∠EAO=![]() 可得答案.
可得答案.
试题解析:(1)当y=0时,﹣2x+2=0,解得:x=1,即点A(1,0),
当x=0时,y=2,即点B(0,2),
如图,直线AB即为所求;

(2)如图,直线l1即为所求,
直线l1的解析式为y=﹣2x+2+4=﹣2x+6,
故答案为y=﹣2x+6;
(3)如图,直线l2即为所求,
∵直线l绕点A顺时针旋转90°得到l2,∴由图可知,点B(0,2)的对应点坐标为(3,1),
设直线l2解析式为y=kx+b,
将点A(1,0)、(3,1)代入,得:![]() ,解得:
,解得: ,
,
∴直线l2的解析式为y=![]() x﹣
x﹣![]() ,当x=0时,y=﹣
,当x=0时,y=﹣![]() ,
,
∴直线l2与y轴的交点E(0,﹣![]() ),∴tan∠CAD=tan∠EAO=
),∴tan∠CAD=tan∠EAO=![]() =
=![]() =
=![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目