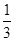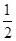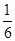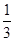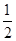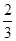题目内容
甲、乙两位同学玩摸球游戏,准备了A、B两个口袋,其中A口袋中放有标号为2,3,5,6的4个球,B口袋中放有标号为1,4,7的3个球.游戏规则:甲从A口袋摸一球,乙从B口袋摸一球,摸出的两球所标数字之差(甲摸取数字﹣乙摸取数字)大于0时甲胜,小于0时乙胜.你认为这个游戏规则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.
公平,理由见解析.
试题分析:游戏公平,理由为:列出表格,得出所有等可能的情况数,找出数字之差大于0,等于0以及小于0时的情况数,求出甲乙两获胜的概率,即可判断不公平,若要使游戏公平,修改规则即可.
试题解析:游戏公平,理由为:
列表得:
| | 2 | 3 | 5 | 6 |
| 1 | (2,1) | (3,1) | (5,1) | (6,1) |
| 4 | (2,4) | (3,4) | (5,4) | (6,4) |
| 7 | (2,7) | (3,7) | (5,7) | (6,7) |
则P甲获胜=
 =
= ,P乙获胜=
,P乙获胜= =
= ,
,∵
 ,
,∴游戏对甲、乙双方是公平的.
考点: 1.游戏公平性;2.列表法与树状图法.

练习册系列答案
相关题目