题目内容
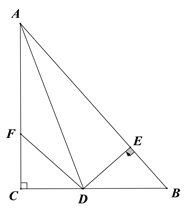
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AF=2,EB=1,求AB的长.

【答案】(1)证明见解析;(2)4
【解析】(1)由AD为角平分线,利用角平分线定理得到DE=DC,再由BD=DF,利用HL得到三角形FCD与三角形BDF全等,利用全等三角形对应边相等即可得证;
(2)利用AAS得到三角形ACD与三角形AED全等,利用全等三角形对应边相等得到AC=AE,由AB=AE+EB,等量代换即可得证.
(1)证明:∵ AD是∠BAC的平分线,∠C=90°,DE⊥AB
∴ DC=DE
∵ BD=DF
∴Rt△DCF≌Rt△DEB
∴CF=EB
(2)解:由(1)知CF=EB=1
∴AC=AF+FC=3
又∵Rt△ACD≌Rt△AED(HL或AAS)
∴AC=AE=3
∴AB=AE+EB=3+1=4
“点睛“此题考查了全等三角形的判定与性质,以及角平分线性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目