Question

（2002•武汉）为了备战世界杯，中国足球队在某次训练中，一队员在距离球门12m处的挑射正好射中了2.4m高的球门横梁，若足球运行的路线是抛物线y=ax²+bx+c（如图所示）则下列结论：①a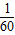＜-，②-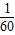＜a＜0，③a-b+c＞0，④0＜b＜-24a，其中正确的结论是（ ）

A．①③
B．①④
C．②③
D．②④

Answer 1

【答案】分析：根据二次函数图象的性质，借助于解不等式即可解答．
解答：解：由抛物线的开口向下知a＜0，
对称轴为x=＞0，
∴a、b异号，即b＞0．
与y轴的交点坐标为（0，2.4），
∴c=2.4
把点（12，0）代入解析式得：
144a+12b+2.4=0．
∴144a=-2.4-12b，12b=-2.4-144a
∴144a＜-2.4，12b＜-144a
∴a＜-，b＜-12a，
∴2b＜-24a，
即b＜-12a，
∴b＜-24a，
∴①④正确，②错误
∵此题是实际问题，
∴x不能取-1，
∴③a-b+c＞0错误．
故选B．
点评：此题考查了学生的综合应用能力，考查了二次函数的图象和性质，还考查了不等式的性质，解题的关键是注意数形结合思想的应用．