题目内容
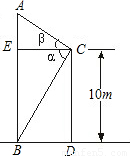
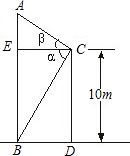
在一座高为10 m的大楼顶C测得旗杆底部B的俯角α为60°,旗杆顶端A的仰角β为20°.(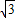 取1.73,tan20°≈0.3646)
取1.73,tan20°≈0.3646)(1)求建筑物与旗杆的水平距离BD;(2)计算旗杆高.(精确到0.1 m)

【答案】分析:首先根据题意分析图形;本题涉及到两个直角三角形,借助公共边CE等价转换,解这两个三角形可得BD的值及AE、BE的值,再利用AB=AE+BE,进而可求出答案.
解答:解:(1)∵∠CBD=α=60°,
∴在Rt△BDC中,
tan∠CBD=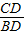 .
.
∴BD=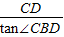 =
=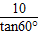 =
=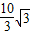 (m).
(m).
(2)设CE⊥AB,垂足为E,
∴CE=BD=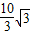 (m).
(m).
在Rt△AEC中,∵tanβ=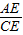 ,
,
∴AE=CE•tanβ=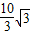 •tan20°≈2.1(m).
•tan20°≈2.1(m).
∴AB=2.1+10=12.1(m),即旗杆高为12.1m.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
解答:解:(1)∵∠CBD=α=60°,
∴在Rt△BDC中,
tan∠CBD=
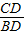 .
.∴BD=
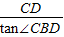 =
=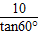 =
=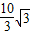 (m).
(m).(2)设CE⊥AB,垂足为E,
∴CE=BD=
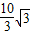 (m).
(m).在Rt△AEC中,∵tanβ=
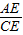 ,
,∴AE=CE•tanβ=
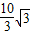 •tan20°≈2.1(m).
•tan20°≈2.1(m).∴AB=2.1+10=12.1(m),即旗杆高为12.1m.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 .73,tan20°≈0.3646)
.73,tan20°≈0.3646) 取1
取1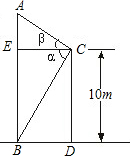 .73,tan20°≈0.3646)
.73,tan20°≈0.3646)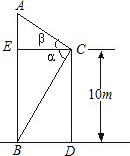
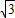 取1.73,tan20°≈0.3646)
取1.73,tan20°≈0.3646)