题目内容
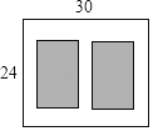
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,设人行通道的宽度为xm,则可列方程为_____.
【答案】(30﹣3x)(24﹣2x)=480.
【解析】
设人行通道的宽度为xm,则两块矩形绿地可合成长为(30-3x)m、宽为(24-2x)m的大矩形,根据矩形的面积公式结合绿地的面积为480m2,即可得出关于x的一元二次方程.
解:设人行通道的宽度为xm,则两块矩形绿地可合成长为(30﹣3x)m、宽为(24﹣2x)m的大矩形,
根据题意得:(30﹣3x)(24﹣2x)=480.
故答案为:(30﹣3x)(24﹣2x)=480.

【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:千帕)随气体体积V(单位:立方米)的变化而变化,P随V的变化情况如下表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出符合表格数据的P关于V的函数表达式 ;
(2)当气球的体积为20立方米时,气球内气体的气压P为多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数表达式,基于安全考虑,气球的体积至少为多少立方米?
【题目】“春节”前夕,某超市购进某种品牌礼品,每盒进价是40元,超市规定每盒售价不得少于45元,设每盒售价为x(元),每天的销售量y(盒),y与x成一次的函数关系,经过市场调查获得部分数据如下表:
每盒售价为x(元) | 45 | 50 | 55 | … |
每天的销售量y(盒) | 450 | 400 | 350 | … |
(1)试求出y与x之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)物价部门规定:这种礼品每盒售价不得高于60元,如果超市想要每天获得不低于5250元的利润,那么超市每天至少销售这种礼品多少盒?