题目内容
(2008•永州)如图,二次函数y=ax2+bx+c(a>0)与坐标轴交于点A、B、C且OA=1,OB=OC=3.(1)求此二次函数的解析式;
(2)写出顶点坐标和对称轴方程;
(3)点M、N在y=ax2+bx+c的图象上(点N在点M的右边),且MN∥x轴,求以MN为直径且与x轴相切的圆的半径.

【答案】分析:(1)由OA=1,OB=OC=3,可知三点的坐标分别为A(-1,0),B(3,0),C(0,-3),用待定系数法求得解析式;
(2)把解析式变换成顶点式,写出坐标;
(3)由(2)知,对称轴为x=1,当MN在x轴下方时,设圆半径为r,则点N的坐标为(1+r,-r),代入解析式求得r的值,同理求得当MN在x轴上方时r的值.
解答:解:(1)依题意A(-1,0),B(3,0),C(0,-3)分别代入y=ax2+bx+c,
解方程组得所求解析式为y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4,
∴顶点坐标(1,-4),对称轴x=1;
(3)设圆半径为r,当MN在x轴下方时,N点坐标为(1+r,-r),
把N点代入y=x2-2x-3得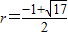 ,
,
同理可得另一种情形,
∴圆的半径为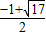 或
或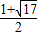 .
.
点评:本题利用了待定系数法求函数的解析式,二次函数的图象与圆的关系,相切的概念求解.
(2)把解析式变换成顶点式,写出坐标;
(3)由(2)知,对称轴为x=1,当MN在x轴下方时,设圆半径为r,则点N的坐标为(1+r,-r),代入解析式求得r的值,同理求得当MN在x轴上方时r的值.
解答:解:(1)依题意A(-1,0),B(3,0),C(0,-3)分别代入y=ax2+bx+c,
解方程组得所求解析式为y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4,
∴顶点坐标(1,-4),对称轴x=1;
(3)设圆半径为r,当MN在x轴下方时,N点坐标为(1+r,-r),
把N点代入y=x2-2x-3得
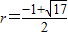 ,
,同理可得另一种情形,
∴圆的半径为
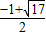 或
或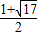 .
.点评:本题利用了待定系数法求函数的解析式,二次函数的图象与圆的关系,相切的概念求解.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目



