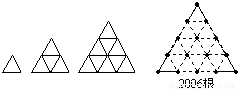题目内容
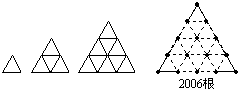 如图,是用火柴棒摆出的一系列三角形图案,按这种方案摆下去,当每边上摆2006根火柴棒时,共需要摆
如图,是用火柴棒摆出的一系列三角形图案,按这种方案摆下去,当每边上摆2006根火柴棒时,共需要摆分析:通过观察前三个图形可以发现其中的规律为:每边上摆n根火柴棒时,需
×n×(n+1)根火柴棒,应用规律解决问题即可.
| 3 |
| 2 |
解答:解:根据题意分析可得:
搭第1个图形需3根火柴,有
×1×(1+1)=3;
搭第2个图形需9根火柴,有
×2×(2+1)=9;
搭第3个图形需18根火柴,有
×3×(3+1)=18;
…;
故当每边上摆2006根火柴棒时,即搭第2006个图形时,需
×2006×(2006+1)=6039063.
搭第1个图形需3根火柴,有
| 3 |
| 2 |
搭第2个图形需9根火柴,有
| 3 |
| 2 |
搭第3个图形需18根火柴,有
| 3 |
| 2 |
…;
故当每边上摆2006根火柴棒时,即搭第2006个图形时,需
| 3 |
| 2 |
点评:此题考查了规律性问题.注意由特殊到一般的分析方法,注意此题的规律为每边上摆n根火柴棒时,需
×n×(n+1)根火柴棒.
| 3 |
| 2 |

练习册系列答案
相关题目

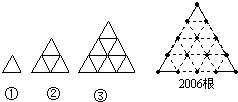
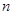 =1时,火柴棒为3根)按这种方法摆下去,当每边上摆10根(即
=1时,火柴棒为3根)按这种方法摆下去,当每边上摆10根(即