题目内容
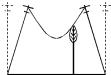2008年我国南方发生重大雪灾，某村地处海拔1 020米，村里的电线断杆以及电杆倾斜多达23处，如图所示就是一处电杆严重倾斜的情况，由于电线上缀满了冰，致使两个电杆都倾斜了26°，电线正好触及一棵高29.5米的大树，已知此树底部离右侧的电杆（电杆高40米，两杆之间距离为50米）20米远，那么此时，电线的最低处离地面约
- A.28.8米
- B.26.3米
- C.25.2米
- D.24.3米
D
分析：以地面的水平线为x轴，两根电杆的中点为坐标原点建立平面直角坐标系，设出函数解析式y=ax2+k，求出图象上点的坐标，进一步求出解析式，利用解析式解答即可．
解答：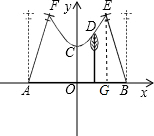
解：作EG⊥x轴，在直角△BEG中，∠BEG=26°，
则EG=BE•cos∠BEG=40•cos26°，BG=BE•sin26°，
则E的坐标是：E（25-40sin26°，40cos26°）．
如图，设函数解析式为y=ax2+k，
把点D（5，29.5），E（25-40sin26°，40cos26°）代入函数解析式得，
，
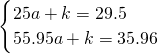解得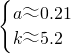
，
因此y=0.21x2+24.3，
所以点C的坐标为（0，24.3）；
即电线的最低处离地面约24.3米．
故选D．
点评：此题考查根据抛物线的特点，建立适当的平面直角坐标系，利用待定系数法求出函数解析式就可以解决问题．
分析：以地面的水平线为x轴，两根电杆的中点为坐标原点建立平面直角坐标系，设出函数解析式y=ax2+k，求出图象上点的坐标，进一步求出解析式，利用解析式解答即可．
解答：
解：作EG⊥x轴，在直角△BEG中，∠BEG=26°，则EG=BE•cos∠BEG=40•cos26°，BG=BE•sin26°，
则E的坐标是：E（25-40sin26°，40cos26°）．
如图，设函数解析式为y=ax2+k，
把点D（5，29.5），E（25-40sin26°，40cos26°）代入函数解析式得，
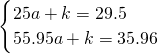，解得
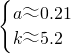，因此y=0.21x2+24.3，
所以点C的坐标为（0，24.3）；
即电线的最低处离地面约24.3米．
故选D．
点评：此题考查根据抛物线的特点，建立适当的平面直角坐标系，利用待定系数法求出函数解析式就可以解决问题．
练习册系列答案
相关题目
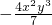的系数是-4
如图，已知AB=AD，∠B=∠D，则BC=DC．请说明理由．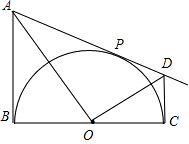
如图，BC是⊙O的直径，AB、AD是⊙O的切线，切点分别为B、P，过C点的切线与AD交于点D，连接AO、DO．
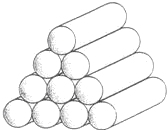（1）10个外径为1dm的钢管以如图方式堆放，为了防雨，需搭建防雨棚，这个防雨棚的高度最低应为多少dm？（取准确值）