题目内容
一个等腰梯形上底等于腰长，下底等于腰长的两倍，那么较小的内角大小为分析：由等腰梯形的性质及题中腰和底的关系，可推出cosD=
=
，从而得出∠D=60°．
| DE |
| AD |
| 1 |
| 2 |
解答：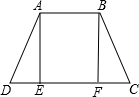
解：如图，AE，BF分别是等腰梯形的高，
∵AB=AD，DC=2AD
∴DE+FC=AD，DE=
AD
∴cosD=
=
∴∠D=60°
即：较小的内角为60°
解：如图，AE，BF分别是等腰梯形的高，∵AB=AD，DC=2AD
∴DE+FC=AD，DE=
| 1 |
| 2 |
∴cosD=
| DE |
| AD |
| 1 |
| 2 |
∴∠D=60°
即：较小的内角为60°
点评：此题主要考查学生对等腰梯形的性质的理解及运用．
练习册系列答案
相关题目
如图，要设计一个等腰梯形的花坛，花坛上底长12米，下底长18米，高8米．