题目内容
保护青少年视力,已为社会所关注,为了调查某初中400名毕业生的视力情况,从中抽测了部分学生的视力,现将抽测数据整理如图:
| 分组 | 频数 | 频率 |
| 0.5-0.8 | 3 | 0.06 |
| 0.8-1.1 | 0.18 | |
| 1.1-1.4 | 15 | 0.30 |
| 1.4-1.7 | ||
| 1.7-2.0 | 2 | 0.04 |
| 合计 | 1.00 |
(1)将表中所缺数据补充完整;______
(2)若视力在1.1以上(含1.1)的均属正常,试估计该校毕业生视力正常的人数约为______人.
解:(1)填表如下:
;
(2)视力在1.1以上的人数=15+21+2=38人,频率=38÷50=0.76,
故该校毕业生视力正常的人数约为400×0.76=304人.
分析:(1)根据各组频率之和为1,可求得1.4--1.7一组的频率为0.42;根据频率等于频数与样本容量的比值;可求得:频数之和为50;进而求得:0.8--1.1的频数为9,1.4--1.7的频数为21;
(2)用样本估计总体,可得:该校毕业生视力正常的人数约为400×(0.42+0.04+0.30)=304人.
点评:本题考查数据的频数与频率的关系,各组频率之和为1,各组频数之和样本容量;频率等于频数与样本容量的比值.
| 分组 | 频数 | 频率 |
| 0.5-0.8 | 3 | 0.06 |
| 0.8-1.1 | 9 | 0.18 |
| 1.1-1.4 | 15 | 0.30 |
| 1.4-1.7 | 21 | 0.42 |
| 1.7-2.0 | 2 | 0.04 |
| 合计 | 50 | 1.00 |
(2)视力在1.1以上的人数=15+21+2=38人,频率=38÷50=0.76,
故该校毕业生视力正常的人数约为400×0.76=304人.
分析:(1)根据各组频率之和为1,可求得1.4--1.7一组的频率为0.42;根据频率等于频数与样本容量的比值;可求得:频数之和为50;进而求得:0.8--1.1的频数为9,1.4--1.7的频数为21;
(2)用样本估计总体,可得:该校毕业生视力正常的人数约为400×(0.42+0.04+0.30)=304人.
点评:本题考查数据的频数与频率的关系,各组频率之和为1,各组频数之和样本容量;频率等于频数与样本容量的比值.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
(2002•荆门)保护青少年视力,已为社会所关注.为了调查某初中400名毕业生的视力情况,从中抽测了部分学生的视力.现将抽测数据整理如下表.
注:表中每组分点含最小值,不含最大值.
(1)将表中所缺数据补充完整;
(2)若视力在1.1以上(含1.1)的均属正常,试估计该校毕业生视力正常的人数约为______人;
(3)这次检测中,能否肯定被检学生视力的中位数在哪一小组内?能否肯定被检学生视力的众数在哪一小组内?(只需填写“能”或“不能”)
| 分组 | 频数 | 频率 |
| 0.5-0.8 | 3 | 0.06 |
| 0.8-1.1 | 0.18 | |
| 1.1-1.4 | 15 | 0.30 |
| 1.4-1.7 |
(1)将表中所缺数据补充完整;
(2)若视力在1.1以上(含1.1)的均属正常,试估计该校毕业生视力正常的人数约为______人;
(3)这次检测中,能否肯定被检学生视力的中位数在哪一小组内?能否肯定被检学生视力的众数在哪一小组内?(只需填写“能”或“不能”)
(2002•荆门)保护青少年视力,已为社会所关注.为了调查某初中400名毕业生的视力情况,从中抽测了部分学生的视力.现将抽测数据整理如下表.
注:表中每组分点含最小值,不含最大值.
(1)将表中所缺数据补充完整;
(2)若视力在1.1以上(含1.1)的均属正常,试估计该校毕业生视力正常的人数约为______人;
(3)这次检测中,能否肯定被检学生视力的中位数在哪一小组内?能否肯定被检学生视力的众数在哪一小组内?(只需填写“能”或“不能”)
| 分组 | 频数 | 频率 |
| 0.5-0.8 | 3 | 0.06 |
| 0.8-1.1 | 0.18 | |
| 1.1-1.4 | 15 | 0.30 |
| 1.4-1.7 |
(1)将表中所缺数据补充完整;
(2)若视力在1.1以上(含1.1)的均属正常,试估计该校毕业生视力正常的人数约为______人;
(3)这次检测中,能否肯定被检学生视力的中位数在哪一小组内?能否肯定被检学生视力的众数在哪一小组内?(只需填写“能”或“不能”)
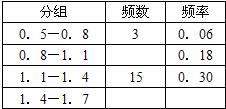
 12、保护青少年视力,已为社会所关注,为了调查某初中400名毕业生的视力情况,从中抽测了部分学生的视力,现将抽测数据整理如图:
12、保护青少年视力,已为社会所关注,为了调查某初中400名毕业生的视力情况,从中抽测了部分学生的视力,现将抽测数据整理如图: