题目内容
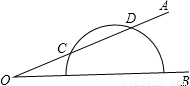
如图,一量角器放置在∠AOB上,角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,则∠AOB的度数是( )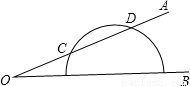
A.20°
B.25°
C.45°
D.55°
【答案】分析:作出量角器所在圆的圆心,设是点E,根据三角形的外角等于不相邻的两个内角的和,以及三角形内角和定理即可求解.
解答: 解:连接CE、ED
解:连接CE、ED
∵角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,即∠4=20°,∠OED=110°
∴∠3=∠OED-∠4=110°-20°=90°.
∴∠1=∠2=45°,∠5=∠2+∠3=45°+90°=135°
故∠AOB=180°-∠5-∠4=180°-135°-20°=25°
故选B.
点评:本题较简单,解答此题的关键是作出辅助线,利用等腰三角形的性质及三角形内角与外角的关系解答.
解答:
 解:连接CE、ED
解:连接CE、ED∵角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,即∠4=20°,∠OED=110°
∴∠3=∠OED-∠4=110°-20°=90°.
∴∠1=∠2=45°,∠5=∠2+∠3=45°+90°=135°
故∠AOB=180°-∠5-∠4=180°-135°-20°=25°
故选B.
点评:本题较简单,解答此题的关键是作出辅助线,利用等腰三角形的性质及三角形内角与外角的关系解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
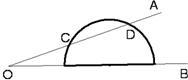 10、如图,一量角器放置在∠AOB上,角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,则∠AOB的度数是( )
10、如图,一量角器放置在∠AOB上,角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,则∠AOB的度数是( )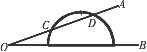
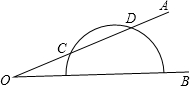 如图,一量角器放置在∠AOB上,角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,则∠AOB的度数是
如图,一量角器放置在∠AOB上,角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,则∠AOB的度数是