题目内容
以前我们曾学过这样的算式:
=1-
,
=
-
,
=
-
,…则
+
+
+…=1-
+
-
+
-
+….
运用这种解题思想计算:
+
+
+…+
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
运用这种解题思想计算:
| 1 |
| (x-1)x |
| 1 |
| x(x+1) |
| 1 |
| (x+1)(x+2) |
| 1 |
| (x+2006)(x+2007) |
分析:根据题中已知的一系列等式,发现
可以拆项为
-
,按照此规律化简所求的式子,抵消后,通分即可求出值.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:原式=
-
+
-
+
-
+…+
-
(4分)
=
-
(7分)
=
(9分)
| 1 |
| x-1 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x+2 |
| 1 |
| x+2006 |
| 1 |
| x+2007 |
=
| 1 |
| x-1 |
| 1 |
| x+2007 |
=
| 2008 |
| (x-1)(x+2007) |
点评:此题考查学生通过观察,猜想,归纳总结的能力.本题的解题思想是对所求的式子拆项后,抵消并通分可得结果.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
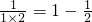 ,
,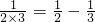 ,
,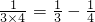 ,…则
,…则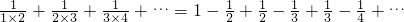 .
.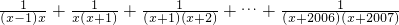 .
. ,…则
,…则 ,运用这种解题思想计算:
,运用这种解题思想计算: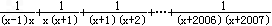 。
。