Question

【题目】如图，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，那么阴影部分的面积是矩形ABCD面积的(　　)

A. B. C. D.

Answer 1

【答案】B

【解析】∵四边形ABCD是矩形，

又∵点O是矩形对角线的交点，

∴OB=OD，

∵四边形ABCD是矩形，

∴AB∥CD，

∴∠ABD=∠CDB，即∠EBO=∠FDO，

∵在△OBE与△ODF中：

，

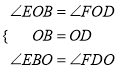∴△OBE≌△ODF (ASA)，

∴△ODF的面积等于△OBE的面积，

∵阴影部分的面积等于△ODF与△AOE的面积之和，

∴阴影部分的面积等于△OBE与△AOE的面积之和，

∵△OBE与△AOE的面积之和等于△AOB的面积，

∴阴影部分的面积等于△AOB的面积.

∵在矩形ABCD中，BD为对角线，

∴在矩形ABCD中，△ABD的面积为矩形ABCD面积的一半，

∵在矩形ABCD中，点O是BD的中点，

∴在△ABD中，△AOB的面积为△ABD的面积的一半，

∴△AOB的面积等于矩形ABCD面积的，

∴阴影部分的面积等于矩形ABCD面积的.

故本题应选B.