题目内容
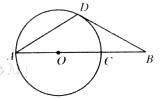
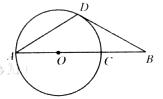
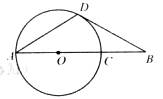
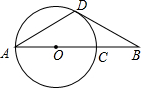 如图,AC为⊙O直径,B为AC延长线上的一点,BD交⊙O于点D,∠BAD=∠B=30°.
如图,AC为⊙O直径,B为AC延长线上的一点,BD交⊙O于点D,∠BAD=∠B=30°.(1)求证:BD是⊙O的切线;
(2)AB=3CB吗?请说明理由.
分析:(1)如图,连接OD,由∠BAD=∠B=30°得到∠ADO=∠BAD=∠B=30°,接着得到∠ADB=120°,∠ODB=90°,然后利用切线的判定方法即可求解;
(2)AB=3CB,由∠ADC=90°得到∠CDB=∠DBC=30°,∠ACD=60°,接着利用直角三角形的性质得到DC=CB,AC=2DC,由此即可证明题目的问题.
(2)AB=3CB,由∠ADC=90°得到∠CDB=∠DBC=30°,∠ACD=60°,接着利用直角三角形的性质得到DC=CB,AC=2DC,由此即可证明题目的问题.
解答:解:(1)如图,连接OD,
∵∠BAD=∠B=30°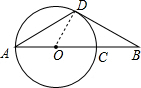 ,
,
∴∠ADO=∠BAD=∠B=30°,
则∠ADB=120°,
∴∠ODB=90°,
又∵D为⊙O上一点,
∴BD是⊙O切线;
(2)AB=3CB
∵∠ADC=90°
∴∠CDB=∠DBC=30°,∠ACD=60°,
则DC=CB,AC=2DC,
即AC=2CB,
所以AB=3CB.
∵∠BAD=∠B=30°
 ,
,∴∠ADO=∠BAD=∠B=30°,
则∠ADB=120°,
∴∠ODB=90°,
又∵D为⊙O上一点,
∴BD是⊙O切线;
(2)AB=3CB
∵∠ADC=90°
∴∠CDB=∠DBC=30°,∠ACD=60°,
则DC=CB,AC=2DC,
即AC=2CB,
所以AB=3CB.
点评:此题主要考查了切线的判定,同时也利用了等腰三角形的性质与判定及含30°的直角三角形的性质,有一定的综合性.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
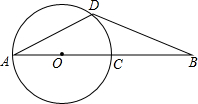 如图,AC为⊙O直径,B为AC延长线上的一点,BD交⊙O于点D,∠BAD=∠B=30°
如图,AC为⊙O直径,B为AC延长线上的一点,BD交⊙O于点D,∠BAD=∠B=30°