Question

正三角形ABC的边长为3cm，一个边长是1cm的正方形EFMN的顶点N与B重合，将正方形如图①所示放置．然后将正方形绕N点顺时针方向旋转，使E点落在AB上，如图②，再将正方形绕E点顺时针方向旋转，使F点落在AB上，如图③…，按照这样的方式旋转下去，直到小正方形有一顶点与B点重合为止，这时小正方形与B点重合的点是    ；小正方形一共旋转的度数是    ．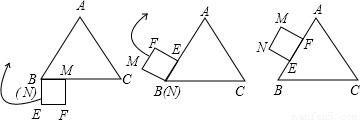

Answer 1

【答案】分析：根据各边长度以及旋转方式得出旋转两周后距离B点1cm，此时EN⊥BC，即可得出直到小正方形有一顶点与B点重合为止，这时小正方形与B点重合的点，利用旋转次数得出旋转角度即可．
解答：解：∵正三角形ABC的边长为3cm，一个边长是1cm的正方形EFMN的顶点N与B重合，将正方形如图①所示放置．然后将正方形绕N点顺时针方向旋转，
∴正方形旋转4次时，正方形本身转动一周，旋转两周后距离B点1cm，此时EN⊥BC，
∴直到小正方形有一顶点与B点重合为止，这时小正方形与B点重合的点是E点，
∵小正方形共旋转9次，有6次旋转90°，有3次绕三角形三个顶点旋转，
得出绕三角形三个顶点旋转时：旋转角度为：360°×3-（3×90°+180°）=630°，
∴小正方形一共旋转的度数是：90°×6+630°=1170°，
故答案为：E，1170°．
点评：此题主要考查了旋转的性质以及正方形性质等知识，根据已知得出旋转的次数以及分别旋转角度是解题关键．