题目内容
为了迎接2008年北京奥运会,某中学组织了一次大型长跑比赛,甲、乙两人在比赛时,路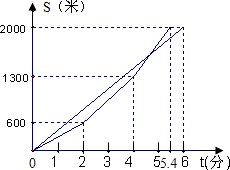 程S(米)与时间t(分钟)的关系如图所示,根据图象答下列问题.
程S(米)与时间t(分钟)的关系如图所示,根据图象答下列问题.
(1)这次长跑比赛的全程是多少米?先到达终点的人比另一个人领先多少分钟?
(2)乙是学校田径队运动员,十分注意比赛技巧,比赛过程分起跑、途中跑、冲刺跑三阶段,经历了两次加速过程.问第4分钟时乙还落后甲多少米?
(3)假设乙在第一次加速后,始终保持这个速度继续前进,那么请你估计甲、乙两人谁先到达终点?请说明你估计的理由.
解:(1)全程2000米;领先0.6分钟;
(2)甲的速度为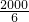 =
=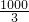 ,
,
第4分钟时甲行了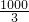 ×4=
×4= ,
,
乙落后甲 -1300=
-1300= 米;
米;
(3)设当2≤t≤4时,乙的图象解析式为S=kt+b,
将(2,600),(4,1300)代入,得
 ,
,
解得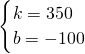 ,
,
∴S=350t-100,
当t=6时,S=350×6-100=2000,
∴甲、乙两人同时到达.
分析:(1)观察图象直接得出结论;
(2)求甲的图象函数关系式,将x=4代入求S的值,与1300作差即可;
(3)设当2≤t≤4时,乙的图象解析式为S=kt+b,将(2,600),(4,1300)代入求一次函数解析式,再把t=6代入求S的值,判断与2000米的大小即可.
点评:本题考查了一次函数的运用.关键是由图象得出相关信息,求直线解析式,运用直线解析式解答题目的其它问题.
(2)甲的速度为
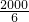 =
=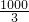 ,
,第4分钟时甲行了
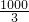 ×4=
×4= ,
,乙落后甲
 -1300=
-1300= 米;
米;(3)设当2≤t≤4时,乙的图象解析式为S=kt+b,
将(2,600),(4,1300)代入,得
 ,
,解得
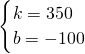 ,
,∴S=350t-100,
当t=6时,S=350×6-100=2000,
∴甲、乙两人同时到达.
分析:(1)观察图象直接得出结论;
(2)求甲的图象函数关系式,将x=4代入求S的值,与1300作差即可;
(3)设当2≤t≤4时,乙的图象解析式为S=kt+b,将(2,600),(4,1300)代入求一次函数解析式,再把t=6代入求S的值,判断与2000米的大小即可.
点评:本题考查了一次函数的运用.关键是由图象得出相关信息,求直线解析式,运用直线解析式解答题目的其它问题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
为了迎接2008年北京奥运会,某校初三学生开展奥运知识比赛,每班派5名学生参加,下表是成绩最好的甲、乙两班参赛学生的比赛数据:
经统计发现两班总分相等.此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)求出这十个比赛数据的众数;
(2)比赛成绩95分以上(包含95分)为优秀,请分别计算两班的优秀率;
(3)哪个班的成绩更稳定?请计算说明.
(4)若以团体总分高低排名次,你认为应该选派哪一个班级参加学校的总决赛更有机会获胜?简述理由.
| 1 | 2 | 3 | 4 | 5 | 总分 | |
| 甲班 | 92 | 97 | 95 | 95 | 96 | 475 |
| 乙班 | 95 | 100 | 93 | 96 | 91 | 475 |
(1)求出这十个比赛数据的众数;
(2)比赛成绩95分以上(包含95分)为优秀,请分别计算两班的优秀率;
(3)哪个班的成绩更稳定?请计算说明.
(4)若以团体总分高低排名次,你认为应该选派哪一个班级参加学校的总决赛更有机会获胜?简述理由.
为了迎接2008年北京奥运会,某校初三学生开展奥运知识比赛,每班派5名学生参加,下表是成绩最好的甲、乙两班参赛学生的比赛数据:
经统计发现两班总分相等.此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)求出这十个比赛数据的众数;
(2)比赛成绩95分以上(包含95分)为优秀,请分别计算两班的优秀率;
(3)哪个班的成绩更稳定?请计算说明.
(4)若以团体总分高低排名次,你认为应该选派哪一个班级参加学校的总决赛更有机会获胜?简述理由.
| 1 | 2 | 3 | 4 | 5 | 总分 | |
| 甲班 | 92 | 97 | 95 | 95 | 96 | 475 |
| 乙班 | 95 | 100 | 93 | 96 | 91 | 475 |
(1)求出这十个比赛数据的众数;
(2)比赛成绩95分以上(包含95分)为优秀,请分别计算两班的优秀率;
(3)哪个班的成绩更稳定?请计算说明.
(4)若以团体总分高低排名次,你认为应该选派哪一个班级参加学校的总决赛更有机会获胜?简述理由.
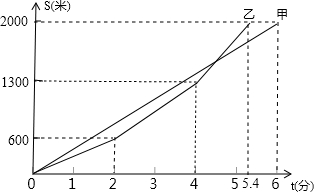
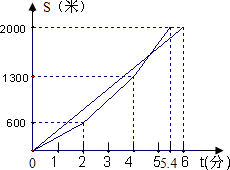 程S(米)与时间t(分钟)的关系如图所示,根据图象答下列问题.
程S(米)与时间t(分钟)的关系如图所示,根据图象答下列问题.