题目内容
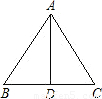
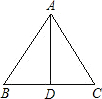 某建筑工地需制作如图所示的三角形支架.己知AB=AC=3m,BC=4m.俗话说“直木顶千斤”,为了增加该三角形支架的耐压程度,需加固一根中柱AD,求中柱AD的长.(精确到0.1m).
某建筑工地需制作如图所示的三角形支架.己知AB=AC=3m,BC=4m.俗话说“直木顶千斤”,为了增加该三角形支架的耐压程度,需加固一根中柱AD,求中柱AD的长.(精确到0.1m).
分析:根据中线的性质求得BD的长,已知AB的长,根据勾股定理求得AD的长.
解答:解:∵AD是BC边的中线,BC=4,
∴BD=CD=
BC=
×4=2.
∵AB=AC=3,
∴AD⊥BC.
在Rt△ABD中,AD=
=
=
≈2.236≈2.2.
答:AD的长约2.2米.
∴BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC=3,
∴AD⊥BC.
在Rt△ABD中,AD=
| AB2-BD2 |
| 32-22 |
| 5 |
答:AD的长约2.2米.
点评:此题考查了中线的性质及勾股定理的运用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
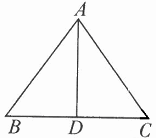
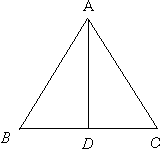
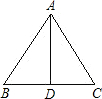 某建筑工地需制作如图所示的三角形支架.己知AB=AC=3m,BC=4m.俗话说“直木顶千斤”,为了增加该三角形支架的耐压程度,需加固一根中柱AD,求中柱AD的长.(精确到0.1m).
某建筑工地需制作如图所示的三角形支架.己知AB=AC=3m,BC=4m.俗话说“直木顶千斤”,为了增加该三角形支架的耐压程度,需加固一根中柱AD,求中柱AD的长.(精确到0.1m).