题目内容
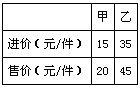
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投人资金不超过4300元,购进甲、乙两种商品,请问乙种商品最多购进多少件?若全部销售完这批商品后获利多少元?(注:获利=售价-进价)
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(2)若商店计划投人资金不超过4300元,购进甲、乙两种商品,请问乙种商品最多购进多少件?若全部销售完这批商品后获利多少元?(注:获利=售价-进价)
分析:(1)等量关系为:甲件数+乙件数=160;甲总利润+乙总利润=1100.
(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量≤4300.
(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量≤4300.
解答:解:(1)设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:
.
解得:
.
答:甲种商品购进100件,乙种商品购进60件.
(2)设甲种商品购进a件,则乙种商品购进(160-a)件.
根据题意得:15a+35(160-a)≤4300,
解不等式,得:a≥65,
∵a为非负整数,∴a取最小值65,即甲种商品最少购进65件,
∴乙种商品最多购进160-95=65(件)
此时获利为:95×5+65×10=1125(元),
答:乙种商品最多购进65件,若全部销售完这批商品后获利1125元.
根据题意得:
|
解得:
|
答:甲种商品购进100件,乙种商品购进60件.
(2)设甲种商品购进a件,则乙种商品购进(160-a)件.
根据题意得:15a+35(160-a)≤4300,
解不等式,得:a≥65,
∵a为非负整数,∴a取最小值65,即甲种商品最少购进65件,
∴乙种商品最多购进160-95=65(件)
此时获利为:95×5+65×10=1125(元),
答:乙种商品最多购进65件,若全部销售完这批商品后获利1125元.
点评:此题主要考查了二元一次方程组的应用以及一元一次不等式的应用,解决本题的关键是读懂题意,找到所求量的等量关系及符合题意的不等关系式组:甲件数+乙件数=160;甲总利润+乙总利润=1100.甲进价×甲数量+乙进价×乙数量≤4300.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:利润=售价-进价)
若商店计划销售完这批商品后能使利润达到1100元,问甲、乙两种商品应分别购进多少件?
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
解方程组:
10.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价),若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?

10.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价),若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
| | 甲 | 乙 |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |