题目内容
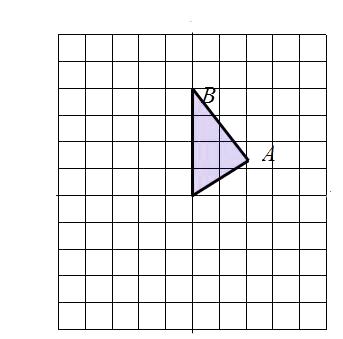
【题目】在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),其中a,b满足 ![]() +|2a﹣5b﹣30|=0.将点B向右平移26个单位长度得到点C,如图①所示.
+|2a﹣5b﹣30|=0.将点B向右平移26个单位长度得到点C,如图①所示.
(1)求点A,B,C的坐标;
(2)点M,N分别为线段BC,OA上的两个动点,点M从点C向左以1.5个单位长度/秒运动,同时点N从点O向点A以2个单位长度/秒运动,如图②所示,设运动时间为t秒(0<t<15).
①当CM<AN时,求t的取值范围;
②是否存在一段时间,使得S四边形MNOB>2S四边形MNAC?若存在,求出t的取值范围;若不存在,说明理由.
【答案】
(1)解:∵ ![]() +|2a﹣5b﹣30=0,且
+|2a﹣5b﹣30=0,且 ![]() ≥0,|2a﹣5b﹣30|≥0,
≥0,|2a﹣5b﹣30|≥0,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴A(30,0),B(0,6),
又∵点C是由点B向右平移26个单位长度得到,
∴C(26,6)
(2)解:①由(1)可知:OA=30,
∵点M从点C向右以1.5个单位长度/秒运动,点N从点O向点A以2个单位长度/秒运动,
∴CM=1.5t,ON=2t,
∴AN=30﹣2t
∵CM<AN,
∴1.5t<30﹣2t,解得t< ![]() ,而0<t<15,
,而0<t<15,
∴0<t< ![]() ;
;
②由题意可知CM=1.5t,ON=2t,
∴BM=BC﹣CM=26﹣1.5t,AN=30﹣2t,
又B(0,6),
∴OB=6,
∴S四边形MNOB= ![]() OB(BM+ON)=3(26﹣1.5t+2t)=3(26+0.5t),S四边形MNAC=
OB(BM+ON)=3(26﹣1.5t+2t)=3(26+0.5t),S四边形MNAC= ![]() OB(AN+CM)=3(30﹣2t+1.5t)=3(30﹣0.5t),
OB(AN+CM)=3(30﹣2t+1.5t)=3(30﹣0.5t),
当S四边形MNOB>2S四边形MNAC时,则有3(26+0.5t)>2×3(30﹣0.5t),解得t> ![]() >15,
>15,
∴不存在使S四边形MNOB>2S四边形MNAC的时间段.
【解析】(1)由条件可求得a、b的值,则可求得A、B两点的坐标,再由平移可求得C点坐标;(2)①用t可分别表示出CM和AN,由条件可得到关于t不等式,可求得t的取值范围;②用t表示出四边形MNOB和四边形MNAC的面积,由条件得到t的不等式,再结合t的取值范围进行判定即可.

 阅读快车系列答案
阅读快车系列答案【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 220 | 180 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.