题目内容
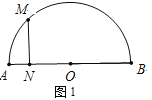
【题目】如图1,半圆O的半径![]() =5cm,点N是半径AO上的一个动点(不与A、O重合),沿AO方向以1cm/s的速度向O点运动,过点N作MN⊥AB,交半圆O于点M,设运动时间为t s.
=5cm,点N是半径AO上的一个动点(不与A、O重合),沿AO方向以1cm/s的速度向O点运动,过点N作MN⊥AB,交半圆O于点M,设运动时间为t s.
(1)求当t等于多少时,MN=3cm?
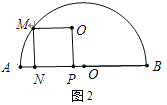
(2)如图2,以MN为边在半圆O内部作正方形MNPQ,使得点P落在AB上,点Q落在半圆内(或半圆上),设正方形MNPQ的面积为S.求S与t之间的函数关系式与自变量t的取值范围.
【答案】(1)当t等于1时,MN=3cm;
(2)S与t之间的函数关系式为![]() ,自变量t的取值范围是:
,自变量t的取值范围是: ![]() .
.
【解析】27. (1)

连接OM
∵MN⊥OA
∴ 在Rt△MNO中,OM=5,MN=3
∴ON=![]() ………………………2分
………………………2分
∴AN=AO-NO=1cm ………………………3分
∴t=1………………………………4分
(2)连接OM
∵AN=t
∴NO=5-t ……………………………5分
∴由勾股定理可得:

MN 2=OM 2-ON 2=![]() ……7分∴
……7分∴![]() …8分
…8分
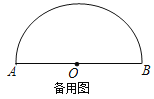
当Q落在半圆上时,如图所示,连接OM、OQ
则OM=OQ
∴Rt△MNO≌Rt△QPO (HL)
∴ON=OP
∵AN=t∴NO=5-t
∴MN=NP=2(5-t)=10-2t……………………………9分
由勾股定理可得:MN2+ON2=OM2 即![]()
解得:t=![]() (舍去)或
(舍去)或![]() …………………10分
…………………10分
∴t的取值范围是: ![]() …………………11分
…………………11分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目