题目内容
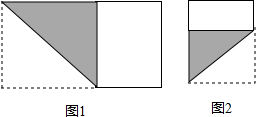
八年级数学课外实践小组进行了一次剪纸探究活动,第1次操作:将一张矩形纸片按如图1所示的方式折叠,剪下一个边长等于此矩形宽度的正方形;第2次操作:把剩下的矩形按如图2所示的方式折叠,剪下一个边长等于此矩形宽度的正方形…如此反复操作下去,直至第n次操作后,剩下的矩形为正方形,则停止操作,将一张长为10cm,宽为acm的矩形纸片(5<a<8)按上述方式操作,若n=3,则a的值为
6
6
.
分析:根据翻折的性质分别求出第1次、第2次、第3次翻折后剩余矩形的长和宽,然后根据n=3时剩下的矩形为正方形列式计算即可得解.
解答:解:第1次翻折,剩余矩形的长为a,宽为10-a,
第2次翻折,剩余矩形的长为10-a,宽为a-(10-a)=2a-10,
第3次翻折,剩余矩形的长为2a-10,宽为10-a-(2a-10)=20-3a,
∵n=3时,剩余矩形为正方形,
∴2a-10=20-3a,
解得a=6.
故答案为:6.
第2次翻折,剩余矩形的长为10-a,宽为a-(10-a)=2a-10,
第3次翻折,剩余矩形的长为2a-10,宽为10-a-(2a-10)=20-3a,
∵n=3时,剩余矩形为正方形,
∴2a-10=20-3a,
解得a=6.
故答案为:6.
点评:本题考查了翻折变换的性质,矩形、正方形的性质,读懂题目信息,分别表示出翻折后剩余矩形的长和宽是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计解析,绘制了如下不完整的统计表和统计图(图).
|
次数 |
10 |
8 |
6 |
5 |
|
人数 |
3 |
a |
2 |
1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?
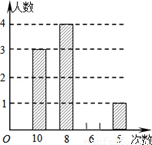
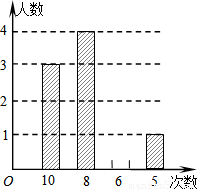 某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计分析,绘制了如下不完整的统计表和统计图(图).
某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计分析,绘制了如下不完整的统计表和统计图(图).| 次数 | 10 | 8 | 6 | 5 |
| 人数 | 3 | a | 2 | 1 |
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?
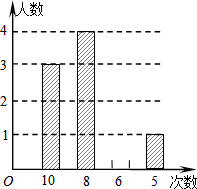 (2013•益阳)某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计分析,绘制了如下不完整的统计表和统计图(图).
(2013•益阳)某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计分析,绘制了如下不完整的统计表和统计图(图).