题目内容
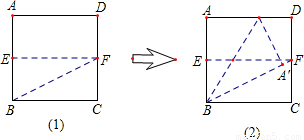
折纸与证明---用纸折出黄金分割点:第一步:如图(1),先将一张正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.
第二步:如图(2),将AB边折到BF上,得到折痕BG,试说明点G为线段AD的黄金分割点(AG>GD)

【答案】分析:连接GF,设正方形的边长为1,由折纸第一步,可知DF= ,在Rt△BCF中,根据勾股定理得出BF=
,在Rt△BCF中,根据勾股定理得出BF=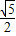 ,则A′F=
,则A′F=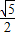 -1.设AG=A'G=x,则GD=1-x,在Rt△A′GF和Rt△DGF中,根据勾股定理由GF不变得出A′F2+A′G2=DF2+DG2,列出关于x的方程,解方程求出x=
-1.设AG=A'G=x,则GD=1-x,在Rt△A′GF和Rt△DGF中,根据勾股定理由GF不变得出A′F2+A′G2=DF2+DG2,列出关于x的方程,解方程求出x=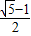 ,即可说明点G是AD的黄金分割点.
,即可说明点G是AD的黄金分割点.
解答: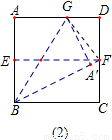 证明:如图,连接GF,设正方形ABCD的边长为1,则DF=
证明:如图,连接GF,设正方形ABCD的边长为1,则DF= .
.
在Rt△BCF中,BF=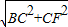 =
=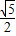 ,
,
则A′F=BF-BA′=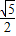 -1.
-1.
设AG=A′G=x,则GD=1-x,
在Rt△A′GF和Rt△DGF中,有A'F2+A'G2=DF2+DG2,
即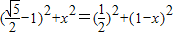 ,
,
解得x=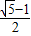 ,
,
即点G是AD的黄金分割点(AG>GD).
点评:本题考查黄金分割的概念:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.
 ,在Rt△BCF中,根据勾股定理得出BF=
,在Rt△BCF中,根据勾股定理得出BF=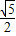 ,则A′F=
,则A′F=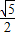 -1.设AG=A'G=x,则GD=1-x,在Rt△A′GF和Rt△DGF中,根据勾股定理由GF不变得出A′F2+A′G2=DF2+DG2,列出关于x的方程,解方程求出x=
-1.设AG=A'G=x,则GD=1-x,在Rt△A′GF和Rt△DGF中,根据勾股定理由GF不变得出A′F2+A′G2=DF2+DG2,列出关于x的方程,解方程求出x=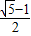 ,即可说明点G是AD的黄金分割点.
,即可说明点G是AD的黄金分割点.解答:
 证明:如图,连接GF,设正方形ABCD的边长为1,则DF=
证明:如图,连接GF,设正方形ABCD的边长为1,则DF= .
.在Rt△BCF中,BF=
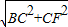 =
=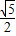 ,
,则A′F=BF-BA′=
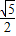 -1.
-1.设AG=A′G=x,则GD=1-x,
在Rt△A′GF和Rt△DGF中,有A'F2+A'G2=DF2+DG2,
即
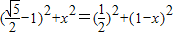 ,
,解得x=
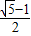 ,
,即点G是AD的黄金分割点(AG>GD).
点评:本题考查黄金分割的概念:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 (2012•利川市一模)折纸与证明---用纸折出黄金分割点:
(2012•利川市一模)折纸与证明---用纸折出黄金分割点: 折纸与证明---用纸折出黄金分割点:
折纸与证明---用纸折出黄金分割点: