题目内容
已知:∠
AOB=60°,OD、OE分别是∠BOC和∠COA的平分线.(1)如下图,OC在∠AOB内部,求∠DOE的度数;
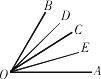
(2)如下图,将OC绕O点旋转到OB的左侧时,OD、OE仍是∠BOC和∠COA的平分线,求此时∠DOE的度数;
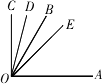
(3)当OC绕O点旋转到OA的下方时,OD、OE分别是∠BOC和∠COA的平分线,∠DOE的度数又是多少?(直接写出结论,不必证明).
答案:
解析:
解析:
|
解: (1)因为OD、OE分别是∠BOC和∠COA的平分线所以∠ COD=所以∠ DOE=∠COD+∠COE=(2)因为OD、OE分别是∠BOC和∠COA的平分线 所以∠ COD=所以∠ DOE=∠COE-∠COD=(3)∠DOE的度数仍然是30°. |

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目