题目内容
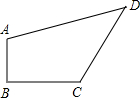 如图四边形ABCD是一块草坪,量得四边长AB=3m,BC=4m,DC=12m,AD=13m,∠B=90°,求这块草坪的面积.
如图四边形ABCD是一块草坪,量得四边长AB=3m,BC=4m,DC=12m,AD=13m,∠B=90°,求这块草坪的面积.
分析:连接AC,由∠B=90°,AB=3cm,BC=4cm可知AC=5cm;由AC、AD、CD的长可判断出△ACD是直角三角形,根据两三角形的面积可求出草坪的面积.
解答: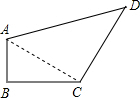 解:在Rt△ABC中,AB=3m,BC=4m,∠B=90°
解:在Rt△ABC中,AB=3m,BC=4m,∠B=90°
由勾股定理得AB2+BC2=AC2
∴AC=5m(2分)
在△ADC中,AC=5m,DC=12m,AD=13m
∴AC2+DC2=169,AD2=169
∴AC2+DC2=AD2(4分)
∠ACD=90°(5分)
四边形的面积=SRt△ABC+SRt△ADC
=
AB×BC+
AC×DC
=
×3×4+
×5×12
=36(m2)
答:这块草坪的面积是36m2.(8分)
 解:在Rt△ABC中,AB=3m,BC=4m,∠B=90°
解:在Rt△ABC中,AB=3m,BC=4m,∠B=90°由勾股定理得AB2+BC2=AC2
∴AC=5m(2分)
在△ADC中,AC=5m,DC=12m,AD=13m
∴AC2+DC2=169,AD2=169
∴AC2+DC2=AD2(4分)
∠ACD=90°(5分)
四边形的面积=SRt△ABC+SRt△ADC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=36(m2)
答:这块草坪的面积是36m2.(8分)
点评:本题是勾股定理在实际中的应用,比较简单.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
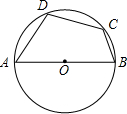 如图四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若再增加一个条件,就可使四边形ABCD成为等腰梯形,你所增加的条件是(只写出一个条件,图中不再增加其他的字母和线段.(给出证明)
如图四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若再增加一个条件,就可使四边形ABCD成为等腰梯形,你所增加的条件是(只写出一个条件,图中不再增加其他的字母和线段.(给出证明)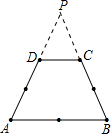 如图四边形ABCD是用7根相同的火柴棒首尾顺次相接围成的梯形,设火柴棒的长度为1,延长AD、BC交于P,若这7根火柴全部保持原位置不动,在PD、PC处能否再添加几根与前面完全相同的火柴棒,使添加的火柴棒在全部用完且不可折的条件下刚好首尾相接拼成△PAB?若不能拼成,请求出梯形ABCD的面积;若能拼成,请求出所添加的火柴棒的总根数,并求出△PDC和△PAB的面积比.
如图四边形ABCD是用7根相同的火柴棒首尾顺次相接围成的梯形,设火柴棒的长度为1,延长AD、BC交于P,若这7根火柴全部保持原位置不动,在PD、PC处能否再添加几根与前面完全相同的火柴棒,使添加的火柴棒在全部用完且不可折的条件下刚好首尾相接拼成△PAB?若不能拼成,请求出梯形ABCD的面积;若能拼成,请求出所添加的火柴棒的总根数,并求出△PDC和△PAB的面积比. ( )
( )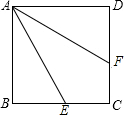 如图四边形ABCD是正方形,点E、F分别在线段BC、DC上,∠BAE=30°.若线段AE绕点A逆时针旋转后与线段AF重合,则旋转的角度是( )
如图四边形ABCD是正方形,点E、F分别在线段BC、DC上,∠BAE=30°.若线段AE绕点A逆时针旋转后与线段AF重合,则旋转的角度是( )