Question

1、以三角形的一条中位线和第三边上的中线为对角线的四边形是（　　）

A、梯形

B、平行四边形

C、菱形

D、矩形

Answer 1

分析：因为这四边形其中的三顶点分别是原三角形的三边的中点，所以这四边形的其中两条邻边是原三角形的中位线，另两条邻边在原三角形的两边上，因此这四边形的两组对边分别平行，所以它是平行四边形．

解答：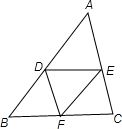
解：如上图：
∵D、E、F分别是三角形的三边的中点
∴DF∥AC，EF∥AB
∵AE、AD分别在AC、AB上
∴DF∥AE，EF∥AD
∴四边形是平行四边形．
故选B．

点评：本题考查平行四边形的判定方法．①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③一组对边平行且相等的四边形是平行四边形；④对角线互相平分的四边形是平行四边形；⑤两组对角分别相等的四边形是平行四边形．