题目内容
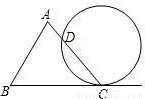
如图,⊙O和⊙O′的公共弦为AB,若AB分别为⊙O和⊙O′的内接正三角形和内接正六边形的一边,AB=2,则两圆公共部分的面积为 .
【答案】分析:连OO′交AB于D,交⊙O于C,根据相交两圆的性质得到OO′垂直平分AB,根据AB为⊙O′内接正六边形的一边,得到△O′AB为等边三角形,即有O′A=AB=2,∠AO′B=60°,根据扇形和三角形的面积公式利用AB与⊙O′所形成的弓形的面积=S扇形O′AB-S△O′AB进行计算;再由AB分别为⊙O的内接正三角形,利用等边三角形的性质和含30度的直角三角形三边的关系得到∴AD=1,∠AOB=2∠ACB=120°,∠AOD=60°,OD=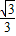 AD=
AD= ,OA=2OD=
,OA=2OD= ,然后利用AB与⊙O所形成的弓形的面积=S扇形OAB-S△OAB,最后把两个结果相加即可得到两圆公共部分的面积.
,然后利用AB与⊙O所形成的弓形的面积=S扇形OAB-S△OAB,最后把两个结果相加即可得到两圆公共部分的面积.
解答: 解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.
解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.
∵AB为⊙O′内接正六边形的一边,
∴△O′AB为等边三角形,
∴O′A=AB=2,∠AO′B=60°,
∴AB与⊙O′所形成的弓形的面积=S扇形O′AB-S△O′AB= -
- ×22=
×22= π-
π- ;
;
又∵AB分别为⊙O的内接正三角形,
∴AD=1,∠AOB=2∠ACB=120°,∠AOD=60°,
∴OD= AD=
AD= ,
,
∴OA=2OD= ,
,
∴AB与⊙O所形成的弓形的面积=S扇形OAB-S△OAB= -
- ×2×
×2× =
= π-
π- ,
,
∴两圆公共部分的面积= π-
π- +
+ π-
π- =
= π-
π- .
.
故答案为 π-
π- .
.
点评:本题考查了扇形的面积公式:S= ;也考查了相交两圆的性质、等边三角形的性质以及含30度的直角三角形三边的关系.
;也考查了相交两圆的性质、等边三角形的性质以及含30度的直角三角形三边的关系.
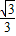 AD=
AD= ,OA=2OD=
,OA=2OD= ,然后利用AB与⊙O所形成的弓形的面积=S扇形OAB-S△OAB,最后把两个结果相加即可得到两圆公共部分的面积.
,然后利用AB与⊙O所形成的弓形的面积=S扇形OAB-S△OAB,最后把两个结果相加即可得到两圆公共部分的面积.解答:
 解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.
解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.∵AB为⊙O′内接正六边形的一边,
∴△O′AB为等边三角形,
∴O′A=AB=2,∠AO′B=60°,
∴AB与⊙O′所形成的弓形的面积=S扇形O′AB-S△O′AB=
 -
- ×22=
×22= π-
π- ;
;又∵AB分别为⊙O的内接正三角形,
∴AD=1,∠AOB=2∠ACB=120°,∠AOD=60°,
∴OD=
 AD=
AD= ,
,∴OA=2OD=
 ,
,∴AB与⊙O所形成的弓形的面积=S扇形OAB-S△OAB=
 -
- ×2×
×2× =
= π-
π- ,
,∴两圆公共部分的面积=
 π-
π- +
+ π-
π- =
= π-
π- .
.故答案为
 π-
π- .
.点评:本题考查了扇形的面积公式:S=
 ;也考查了相交两圆的性质、等边三角形的性质以及含30度的直角三角形三边的关系.
;也考查了相交两圆的性质、等边三角形的性质以及含30度的直角三角形三边的关系. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
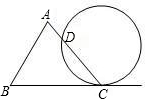 如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则
如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则 |
| CD |
| A、50° | B、60° |
| C、100° | D、120° |
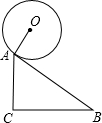 如图为斜面和圆柱形油桶的截面图,斜面AB=5,A点垂直高度AC=3米,油桶的半径为1米,当油桶与斜面相切于A处时,求油桶最高点的高度?
如图为斜面和圆柱形油桶的截面图,斜面AB=5,A点垂直高度AC=3米,油桶的半径为1米,当油桶与斜面相切于A处时,求油桶最高点的高度?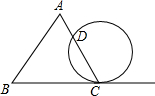 如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则
如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则
 的度数为何( )
的度数为何( )