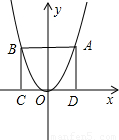��Ŀ����
��ͼ��ʾ��ijͬѧ��̽�����κ���ͼ��ʱ����ֱ��y=mƽ����x�ᣬ�����κ���y=x2��ͼ����A��B���㣬��AC��BD�ֱ�ֱ��x�ᣬ�����ı���ABCD�������Σ���1����m��ֵ��A��B��������ꣻ
��2����ͼ��ʾ���������ߡ�y=x2����Ϊ��y=x2-2x+2����ֱ��CD���������ߵĶ���P��x��ƽ�У�������ϵ���䣬��m��ֵ��A��B��������꣮
��3����ͼ��ʾ����ͼ�еĸ�Ϊ��y=ax2+bx+c��a��0����������ϵ���䣬��ֱ��д��m��ֵ��A��B��
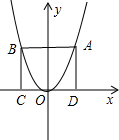 ������꣨�ú���a��b��c�Ĵ���ʽ��ʾ��
������꣨�ú���a��b��c�Ĵ���ʽ��ʾ��[��ʾ��������y=ax2+bx+c�Ķ�������Ϊ��-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
��������1�����������ε����ʺͶ��κ����ĶԳ��Խ���һ�ʣ�
��2�����䷽�����y=x2-2x+2�Ķ������꣬��m��ʾA��B��������꣮������һ����뺯������ʽ�����m��ֵ������ý⣻
��3������������y=ax2�����m=
��A��
��
����B��-
��
��������������y=ax2+bx+c�������꣨-
��
��ƽ���������ã�
��2�����䷽�����y=x2-2x+2�Ķ������꣬��m��ʾA��B��������꣮������һ����뺯������ʽ�����m��ֵ������ý⣻
��3������������y=ax2�����m=
| 4 |
| a |
| 2 |
| a |
| 4 |
| a |
| 2 |
| a |
| 4 |
| a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
����⣺��1�����ı���ABCD�������Σ���������y=x2�ĶԳ��Կ�֪��OD=
AD
�����A������
m��m����
����y=x2��
��m=(
m)2
���m1=0����ȥ����m2=4��
��m��ֵ��4����A������Ϊ��2��4����
�������ߵĶԳ��ԣ��ɵ�B������Ϊ��-2��4����
��2����ͼ��
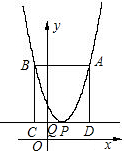 ��y=x2-2x+2=��x-1��2+1��
��y=x2-2x+2=��x-1��2+1��
�������ߵĶ���P����Ϊ��1��1����
�����⣬��A��������Ϊm��
��AD=m-1��
��ֱ��CD��y�ύ��ΪQ��
��DQ=
+1=
m+
��
���A��������
m+
��m����
����y=x2-2x+2��
������m2-6m+5=0��
���m1=1����ȥ����m2=5��
��m��ֵΪ5����A������Ϊ��3��5��
���������ߵĶԳ��ԣ�����õ�B������Ϊ��-1��5����
��3��m=
��
A��
��
����
B��
��
����
��������y=ax2�����m=
��
A��B��������ΪA��
��
����B��-
��
����
��A��B���������ƣ�-
������λ�������ƣ�
�������
������A��
��
����B��
��
����
| 1 |
| 2 |
�����A������
| 1 |
| 2 |
����y=x2��
��m=(
| 1 |
| 2 |
���m1=0����ȥ����m2=4��
��m��ֵ��4����A������Ϊ��2��4����
�������ߵĶԳ��ԣ��ɵ�B������Ϊ��-2��4����
��2����ͼ��
 ��y=x2-2x+2=��x-1��2+1��
��y=x2-2x+2=��x-1��2+1���������ߵĶ���P����Ϊ��1��1����
�����⣬��A��������Ϊm��
��AD=m-1��
��ֱ��CD��y�ύ��ΪQ��
��DQ=
| m-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
���A��������
| 1 |
| 2 |
| 1 |
| 2 |
����y=x2-2x+2��
������m2-6m+5=0��
���m1=1����ȥ����m2=5��
��m��ֵΪ5����A������Ϊ��3��5��
���������ߵĶԳ��ԣ�����õ�B������Ϊ��-1��5����
��3��m=
| 4ac-b2+16 |
| 4a |
A��
| -b+4 |
| 2a |
| 4ac-b2+16 |
| 4a |
B��
| -b-4 |
| 2a |
| 4ac-b2+16 |
| 4a |
��������y=ax2�����m=
| 4 |
| a |
A��B��������ΪA��
| 2 |
| a |
| 4 |
| a |
| 2 |
| a |
| 4 |
| a |
��A��B���������ƣ�-
| b |
| 2a |
| 4ac-b2 |
| 4a |
������A��
| -b+4 |
| 2a |
| 4ac-b2+16 |
| 4a |
| -b-4 |
| 2a |
| 4ac-b2+16 |
| 4a |
�����������Ƕ��κ������ۺ����ͣ������漰����֪ʶ���������ߵĶ��㹫ʽ�������ߵĶԳ��Լ�ͼ���ƽ�ƣ�������Ҫ���ͼ�μ�ʵ��������

��ϰ��ϵ�д�
 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
�����Ŀ
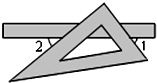 11����ͼ��ʾ��ijͬѧ�ڿ��������⽫һ�����ǰ��ֱ�ǵ�����ֱ���ϣ����1+��2�Ķ�����
11����ͼ��ʾ��ijͬѧ�ڿ��������⽫һ�����ǰ��ֱ�ǵ�����ֱ���ϣ����1+��2�Ķ�����
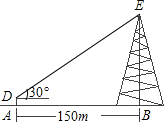 ��ͼ��ʾ��ijͬѧ��������150��A�����ò�������������������Ϊ30�㣮��֪������AD=1.56�ף�������BE�ĸߣ�����ȷ��0.1�ף���������ʱ����ֵȡ1.73��
��ͼ��ʾ��ijͬѧ��������150��A�����ò�������������������Ϊ30�㣮��֪������AD=1.56�ף�������BE�ĸߣ�����ȷ��0.1�ף���������ʱ����ֵȡ1.73��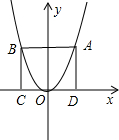 ������꣨�ú���a��b��c�Ĵ���ʽ��ʾ��
������꣨�ú���a��b��c�Ĵ���ʽ��ʾ�� ��
�� �����Գ���Ϊ
�����Գ���Ϊ ]��
]��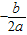 ��
��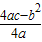 �����Գ���Ϊ
�����Գ���Ϊ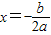 ]��
]��