题目内容
图是一个长为2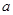 ,宽为2
,宽为2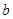 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.
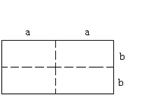
(1)求出图的长方形面积;
(2)将四块小长方形拼成一个图的正方形.利用阴影部分面积的不同表示方法,直接写出代数式(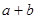 )2、(
)2、(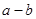 )2、
)2、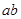 之间的等量关系;
之间的等量关系;
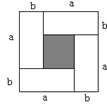
(3)把四块小长方形不重叠地放在一个长方形的内部(如图),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含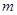 、
、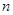 的代数式表示).
的代数式表示).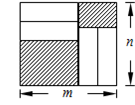
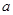 ,宽为2
,宽为2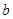 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.
(1)求出图的长方形面积;
(2)将四块小长方形拼成一个图的正方形.利用阴影部分面积的不同表示方法,直接写出代数式(
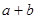 )2、(
)2、(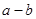 )2、
)2、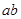 之间的等量关系;
之间的等量关系;
(3)把四块小长方形不重叠地放在一个长方形的内部(如图),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含
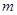 、
、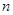 的代数式表示).
的代数式表示).
(1)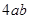 (2)
(2)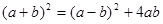 (3)
(3)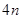
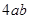 (2)
(2)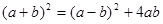 (3)
(3)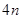
试题分析:(1)依题意知原长方形面积=2a×2b=4ab
(2)依题意知a+b为新拼成大正方形的边长,a-b为阴影小正方形的边长。而大正方形面积=阴影小正方形面积+四个小长方形面积。所以可得
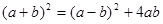
(3)依题意知上面部分的阴影周长为:2(n-a+m-a)
下面部分的阴影周长为:2(m-2b+n-2b)
总周长为:4m+4n-4a-8b又a+2b=m总周长为4n;
点评:本题难度中等,主要考查学生对代数式解决几何问题的综合运用能力,为中考常考题型,要注意躲培养数形结合思想,并灵活运用到考试中去。

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
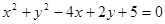 ,则x+y=______。
,则x+y=______。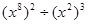 的结果是( )
的结果是( )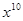
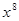
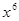
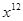
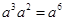
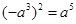
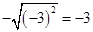


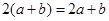
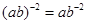
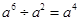
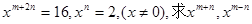 的值
的值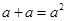
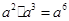

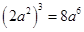
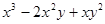 .
.