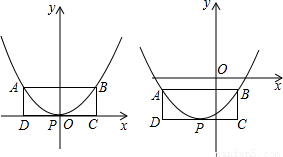题目内容
如左图,抛物线y=x2的顶点为P,A、B是抛物线上两点,AB∥x轴,四边形ABCD为矩形,CD边经过点P,AB=2AD.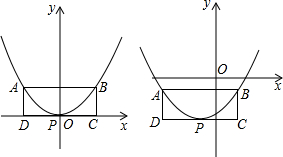
(1)求矩形ABCD的面积;
(2)如图,若将抛物线“y=x2”,改为抛物线“y=x2+bx+c”,其他条件不变,请猜想矩形ABCD的面积;
(3)若将抛物线“y=x2+bx+c”改为抛物线“y=ax2+bx+c”,其他条件不变,请猜想矩形ABCD的面积(用a、b、c表示,并直接写出答案).
分析:(1)根据抛物线的特点知P(0,0),可设OD=AD=m,根据AB=2AD,可分别表示出D、A的坐标,由于A在抛物线上,将其坐标代入抛物线的解析式中,可求得m的值,进而可得到矩形的面积.
(2)参照(1)的思路,首先表示出P点坐标,设DP=AD=m,然后表示出A点的坐标,再将其代入抛物线的解析式中,求得m的值,进而可求出矩形ABCD的面积.
(3)方法同(2).
(2)参照(1)的思路,首先表示出P点坐标,设DP=AD=m,然后表示出A点的坐标,再将其代入抛物线的解析式中,求得m的值,进而可求出矩形ABCD的面积.
(3)方法同(2).
解答:解:(1)∵抛物线y=x2的顶点为P,
∴P(0,0);
设DP=AD=m,则AB=CD=2m;
∴D(-m,0),A(-m,m),
由于点A在抛物线的图象上,则:
(-m)2=m,
解得m=0(舍去),m=1,
∴矩形ABCD的面积为:AB•AD=2m2=2.
(2)矩形的面积不变,仍为2,理由如下:
易知P(-
,
),
设DP=AD=m,同(1)可得A(-
-m,
+m),
代入抛物线的解析式中,得:
(-
-m)2+b(-
-m)+c=
+m,
整理得:m2=m,
解得m=0(舍去),m=1;
故矩形ABCD的面积为:AB•AD=2m2=2.
(3)矩形的面积为
,理由如下:
设DP=AD=m,同(1)(2)可得:A(-
-m,
+m);
代入抛物线的解析式中,得:
a(-
-m)2+b(-
-m)+c=
+m,
整理得:am2=m,
解得m=0(舍去),m=
;
故矩形ABCD的面积为:AB•AD=2m2=
.
∴P(0,0);
设DP=AD=m,则AB=CD=2m;
∴D(-m,0),A(-m,m),
由于点A在抛物线的图象上,则:
(-m)2=m,
解得m=0(舍去),m=1,
∴矩形ABCD的面积为:AB•AD=2m2=2.
(2)矩形的面积不变,仍为2,理由如下:
易知P(-
| b |
| 2 |
| 4c-b2 |
| 4 |
设DP=AD=m,同(1)可得A(-
| b |
| 2 |
| 4c-b2 |
| 4 |
代入抛物线的解析式中,得:
(-
| b |
| 2 |
| b |
| 2 |
| 4c-b2 |
| 4 |
整理得:m2=m,
解得m=0(舍去),m=1;
故矩形ABCD的面积为:AB•AD=2m2=2.
(3)矩形的面积为
| 2 |
| a2 |
设DP=AD=m,同(1)(2)可得:A(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
代入抛物线的解析式中,得:
a(-
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
整理得:am2=m,
解得m=0(舍去),m=
| 1 |
| a |
故矩形ABCD的面积为:AB•AD=2m2=
| 2 |
| a2 |
点评:解决此题的关键,是能够理解抛物线和矩形的对称性,把握好“AB=2AD”这个条件,难度适中.

练习册系列答案
相关题目