题目内容
用配方法解下列方程时,配方正确的是
- A.x2-2x+5=0化为(x-2)2=9
- B.x2+3=4化为(x-2)2=7
- C.x2+3x+2=0化为(x+3)2=

- D.2x2-7x-4=0化为(x-
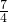 )2=
)2=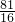
D
分析:把A,B,C,D四个方程分别进行配方,与所给结果进行比较,然后作出选择.
解答:A、x2-2x+5=0,
x2-2x=-5,
x2-2x+1=6,
(x-1)2=6,
故本选项错误;
B、x2+3=4x,
x2-4x=-3,
x2-4x+4=-3+4,
(x-2)2=1,
故本选项错误;
C、x2+3x+2=0,
x2+3x=-2,
x2+3x+ =-2+
=-2+ ,
,
 =
= .
.
故本选项错误;
D、2x2-7x-4=0,
x2- x=2,
x=2,
x2- x+
x+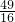 =2+
=2+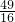 ,
,
 =
=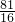 .
.
正确.
故选D.
点评:本题考查的是用配方法解一元二次方程,配方过程中先把二次项系数化成1,常数项移到右边,然后两边加上一次项系数一半的平方,把方程的左边配成完全平方的形式.
分析:把A,B,C,D四个方程分别进行配方,与所给结果进行比较,然后作出选择.
解答:A、x2-2x+5=0,
x2-2x=-5,
x2-2x+1=6,
(x-1)2=6,
故本选项错误;
B、x2+3=4x,
x2-4x=-3,
x2-4x+4=-3+4,
(x-2)2=1,
故本选项错误;
C、x2+3x+2=0,
x2+3x=-2,
x2+3x+
 =-2+
=-2+ ,
, =
= .
.故本选项错误;
D、2x2-7x-4=0,
x2-
 x=2,
x=2,x2-
 x+
x+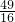 =2+
=2+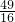 ,
, =
=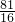 .
.正确.
故选D.
点评:本题考查的是用配方法解一元二次方程,配方过程中先把二次项系数化成1,常数项移到右边,然后两边加上一次项系数一半的平方,把方程的左边配成完全平方的形式.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
用配方法解下列方程时,配方正确的是( )
| A、x2-2x+5=0化为(x-2)2=9 | ||||
| B、x2+3=4化为(x-2)2=7 | ||||
C、x2+3x+2=0化为(x+3)2=
| ||||
D、2x2-7x-4=0化为(x-
|
用配方法解下列方程时,配方有错误的是( )
| A、x2-6x+4=0化为(x-3)2=5 | ||||
B、2m2+m-1=0化为(m+
| ||||
C、3y2-4y-2=0化为(y-
| ||||
D、2t2-3t-2=0化为(t-
|