题目内容
 如图,两个完全相同的等腰直角三角形,左图中正方形的面积是2004平方厘米,那么右图中正方形的面积是
如图,两个完全相同的等腰直角三角形,左图中正方形的面积是2004平方厘米,那么右图中正方形的面积是分析:根据第一个图形中正方形EFNM的面积,可知等腰直角三角形ABC的腰长,第二个图形中正方形ADQG的边长为等腰直角三角形腰长的一半,进而可得出右图中正方形的面积.
解答: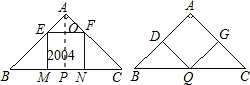 解:设正方形EFNM的边长为2a
解:设正方形EFNM的边长为2a
∵OE=a,AE=
a,BE=
EM=2
a,
∴AB=3
a
∵正方形EFNP的面积为2004,
即(2a)2=2004,
∴a2=501,
∵AG=GQ=
AB,
∴正方形ADQG的面积为:GQ2=(
AB)2=
AB2=
×(3
a)2=
a2=
×501=2254.5,
∴正方形的面积为2254.5平方厘米.
故答案为2254.5.
 解:设正方形EFNM的边长为2a
解:设正方形EFNM的边长为2a∵OE=a,AE=
| 2 |
| 2 |
| 2 |
∴AB=3
| 2 |
∵正方形EFNP的面积为2004,
即(2a)2=2004,
∴a2=501,
∵AG=GQ=
| 1 |
| 2 |
∴正方形ADQG的面积为:GQ2=(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
∴正方形的面积为2254.5平方厘米.
故答案为2254.5.
点评:解答本题要充分利用正方形和等腰直角三角形的特殊性质.

练习册系列答案
相关题目
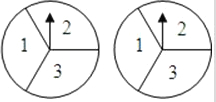 小刚与小亮一起玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘分成面积相等的三个区域,分别用“1”、“2”、“3”表示.固定指针,同时转动两个转盘,任其自由停止.若两指针指的数字和为奇数,则小刚获胜;否则,小亮获胜.则在该游戏中小刚获胜的概率是
小刚与小亮一起玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘分成面积相等的三个区域,分别用“1”、“2”、“3”表示.固定指针,同时转动两个转盘,任其自由停止.若两指针指的数字和为奇数,则小刚获胜;否则,小亮获胜.则在该游戏中小刚获胜的概率是
 (2013•湖北)如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是
(2013•湖北)如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是 小芳和小欣玩一种转盘游戏,如图是两个完全相同的转盘,转盘一被分成面积相等的三个扇形,用数字“1”“2”“3”表示,转盘二被分成面积相等的四个扇形,用数字“1”“2”“3”“4”表示,固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字之积为偶数,则小芳获胜;若两指针所指数字之积为奇数,则小欣获胜;若其中一个指针指向扇形的分界线,则都重转一次.你认为游戏是否公平?请说明理由.若不公平,请你修改游戏规则,使游戏公平.
小芳和小欣玩一种转盘游戏,如图是两个完全相同的转盘,转盘一被分成面积相等的三个扇形,用数字“1”“2”“3”表示,转盘二被分成面积相等的四个扇形,用数字“1”“2”“3”“4”表示,固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字之积为偶数,则小芳获胜;若两指针所指数字之积为奇数,则小欣获胜;若其中一个指针指向扇形的分界线,则都重转一次.你认为游戏是否公平?请说明理由.若不公平,请你修改游戏规则,使游戏公平.