题目内容
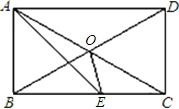 已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,∠AEO=
已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,∠AEO=分析:根据矩形的性质可得:OB=OC,AD∥BC,∠ABC=∠BAD=90°,又由AE平分∠BAD,∠AOD=120°,即可求得:∠OBE与∠AEB的度数,以及△OAB是等边三角形,△ABE是等腰三角形,即可得:△OBE是等腰三角形,求得∠OEB的度数,则问题得解.
解答:解:∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=∠BAD=90°,AC=BD,OB=
BD,OC=
AC,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠BOC=∠AOD=120°,
∴∠OBC=30°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=45°,
∴∠AEB=∠EAD=∠BAE=45°,
∴AB=BE,
∵∠AOD=120°,
∴∠AOB=60°,
∴AB=OA=OB,
∴OB=BE,
∴∠BOE=∠BEO,
∴∠OEB=75°,
∴∠AEO=∠OEB-∠AEB=75°-45°=30°.
故答案为:30°.
∴AD∥BC,∠ABC=∠BAD=90°,AC=BD,OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴OB=OC,
∴∠OBC=∠OCB,
∵∠BOC=∠AOD=120°,
∴∠OBC=30°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=45°,
∴∠AEB=∠EAD=∠BAE=45°,
∴AB=BE,
∵∠AOD=120°,
∴∠AOB=60°,
∴AB=OA=OB,
∴OB=BE,
∴∠BOE=∠BEO,
∴∠OEB=75°,
∴∠AEO=∠OEB-∠AEB=75°-45°=30°.
故答案为:30°.
点评:此题考查了矩形的性质.注意由平行线与角平分线则可构造等腰三角形,还要注意数形结合思想的应用.

练习册系列答案
相关题目
 27、已知:如图,O是矩形ABCD的对角线的交点,BE∥AC,CE∥BD,试说明OE与CB互相垂直平分.
27、已知:如图,O是矩形ABCD的对角线的交点,BE∥AC,CE∥BD,试说明OE与CB互相垂直平分.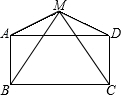 已知:如图,M是矩形ABCD外一点,连接MB、MC、MA、MD,且MA=MD.
已知:如图,M是矩形ABCD外一点,连接MB、MC、MA、MD,且MA=MD.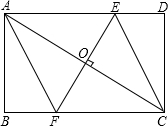 已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F.
已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F. 已知:如图,P是矩形ABCD的CD边上一点,PE⊥AC于E,PF⊥BD于F,AC=15,BC=8,求PE+PF.
已知:如图,P是矩形ABCD的CD边上一点,PE⊥AC于E,PF⊥BD于F,AC=15,BC=8,求PE+PF.