题目内容
 如图,已知?ABED与?AFCD,B、E、F、C在同一直线上,AF⊥DE于G,AG=3cm,DG=4cm.S□ABED=36cm2,则四边形ABCD的周长为
如图,已知?ABED与?AFCD,B、E、F、C在同一直线上,AF⊥DE于G,AG=3cm,DG=4cm.S□ABED=36cm2,则四边形ABCD的周长为
- A.49cm
- B.43cm
- C.41cm
- D.46cm
D
分析:由于AG=3cm,DG=4cm,AG是平行四边形ABED的高,DG是平行四边形AFCD的高,又两平行四边形面积为36,由此可以求出DE,AB,CD,AF又△AGD是直角三角形根据勾股定理可以求出AD,BE,CF,然后延长CD与BA延长线交于H,可得△BHC是直角三角形,然后利用勾股定理和已知条件可以求出CH,BH,接着求出BC,最后就可以求出ABCD的周长.
解答: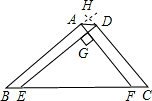 解:∵AG=3cm,DG=4cm,
解:∵AG=3cm,DG=4cm,
∴AG是平行四边形ABED的高,DG是平行四边形AFCD的高,
又两个平行四边形面积为36,
∴DE=AB=12cm,CD=AF=9cm,
又△AGD是直角三角形,
∴AD=BE=CF=5cm,
如图,延长CD与BA延长线交于H,
可得CH=CD+DH=CD+AG=12cm,BH=ED+DG=16cm,
而△BHC是直角三角形,
则BC=20cm,
∴ABCD周长为AB+BC+CD+DA=12+20+9+5=46cm.
故选D.
点评:主要考查了平行四边形的基本性质和平行四边形面积的求法.本题的解题关键是利用面积求出各边的长,从而求出周长.
分析:由于AG=3cm,DG=4cm,AG是平行四边形ABED的高,DG是平行四边形AFCD的高,又两平行四边形面积为36,由此可以求出DE,AB,CD,AF又△AGD是直角三角形根据勾股定理可以求出AD,BE,CF,然后延长CD与BA延长线交于H,可得△BHC是直角三角形,然后利用勾股定理和已知条件可以求出CH,BH,接着求出BC,最后就可以求出ABCD的周长.
解答:
 解:∵AG=3cm,DG=4cm,
解:∵AG=3cm,DG=4cm,∴AG是平行四边形ABED的高,DG是平行四边形AFCD的高,
又两个平行四边形面积为36,
∴DE=AB=12cm,CD=AF=9cm,
又△AGD是直角三角形,
∴AD=BE=CF=5cm,
如图,延长CD与BA延长线交于H,
可得CH=CD+DH=CD+AG=12cm,BH=ED+DG=16cm,
而△BHC是直角三角形,
则BC=20cm,
∴ABCD周长为AB+BC+CD+DA=12+20+9+5=46cm.
故选D.
点评:主要考查了平行四边形的基本性质和平行四边形面积的求法.本题的解题关键是利用面积求出各边的长,从而求出周长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 10、如图,已知?ABED与?AFCD,B、E、F、C在同一直线上,AF⊥DE于G,AG=3cm,DG=4cm.S□ABED=36cm2,则四边形ABCD的周长为( )
10、如图,已知?ABED与?AFCD,B、E、F、C在同一直线上,AF⊥DE于G,AG=3cm,DG=4cm.S□ABED=36cm2,则四边形ABCD的周长为( ) 4、如图,已知正方形ABED与正方形BCFE,现从A,B,C,D,E,F六个点中任取三个点,使得这三个点能作为直角三角形的三个顶点,则这样的直角三角形共有( )
4、如图,已知正方形ABED与正方形BCFE,现从A,B,C,D,E,F六个点中任取三个点,使得这三个点能作为直角三角形的三个顶点,则这样的直角三角形共有( )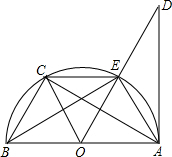 (2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
(2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
