题目内容
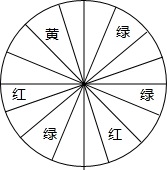 如图,某超市为了吸引顾客,设立了一个可以抽奖转盘,并规定,顾客每购买80元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准黄、红或绿色区域,就可以分别获得40元、30元、20元的购物券(转盘被等分成16个扇形).
如图,某超市为了吸引顾客,设立了一个可以抽奖转盘,并规定,顾客每购买80元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准黄、红或绿色区域,就可以分别获得40元、30元、20元的购物券(转盘被等分成16个扇形).(1)甲顾客消费60元,是否可获得转动转盘的机会?
(2)乙顾客消费100元,他获得购物券的概率是多少?他得到40元、30元、20元购物券的概率分别是多少?
分析:(1)根据顾客每购买80元的商品,就能获得一次转动转盘的机会可知,60元达不到抽奖的条件.
(2)根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.
(2)根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.
解答:解:(1)甲顾客消费额60元小于80元,所以由已知得甲顾客不能获得转动转盘的机会-----(3分);
(2)乙顾客消费额在80到160元之间,因此可以获得转动转盘的机会-----(4分);
转盘被等分成16个扇形,、其中1个是黄色,2个是红色,3个是绿色.转盘停滞后,指针落到每一个扇形的可能性都相等,-----(6分)
因此对于 乙顾客来说
P(获得购物券)=
=
-------(7分);
P(获得40元购物券)=
-------(8分);
P(获得30元购物券)=
=
-------(9分);
P(获得20元购物券)=
------(10分);
(2)乙顾客消费额在80到160元之间,因此可以获得转动转盘的机会-----(4分);
转盘被等分成16个扇形,、其中1个是黄色,2个是红色,3个是绿色.转盘停滞后,指针落到每一个扇形的可能性都相等,-----(6分)
因此对于 乙顾客来说
P(获得购物券)=
| 1+2+3 |
| 16 |
| 3 |
| 8 |
P(获得40元购物券)=
| 1 |
| 16 |
P(获得30元购物券)=
| 2 |
| 16 |
| 1 |
| 8 |
P(获得20元购物券)=
| 3 |
| 16 |
点评:本题考查概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 7、“十•一”假期,某超市为了吸引顾客,设立了一个转盘游戏进行摇奖活动,并规定顾客每购买200元商品,就获得一次转盘机会,小亮根据摇奖情况制作了一个统计图(如图),请你求出每转动一次转盘获得购物券的平均数是( )
7、“十•一”假期,某超市为了吸引顾客,设立了一个转盘游戏进行摇奖活动,并规定顾客每购买200元商品,就获得一次转盘机会,小亮根据摇奖情况制作了一个统计图(如图),请你求出每转动一次转盘获得购物券的平均数是( )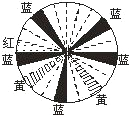 某超市为了吸引顾客,设立了一个可以自由转动的转盘(如图),红色区为一等奖,黄色区为二等奖,蓝色区为三等奖,那么转到二等奖的概率是
某超市为了吸引顾客,设立了一个可以自由转动的转盘(如图),红色区为一等奖,黄色区为二等奖,蓝色区为三等奖,那么转到二等奖的概率是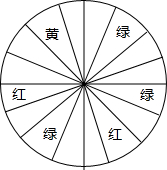 如图,某超市为了吸引顾客,设立了一个可以抽奖转盘,并规定,顾客每购买80元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准黄、红或绿色区域,就可以分别获得40元、30元、20元的购物券(转盘被等分成16个扇形).
如图,某超市为了吸引顾客,设立了一个可以抽奖转盘,并规定,顾客每购买80元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准黄、红或绿色区域,就可以分别获得40元、30元、20元的购物券(转盘被等分成16个扇形).