题目内容
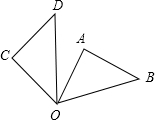
如图,将正方形ABCD以点B为旋转中心顺时针旋转120°得到正方形A′BC′D′,DO⊥C′A′于O,若A′O=
-1,则正方形ABCD的边长为______.

| 3 |

作BE⊥OD于点E.
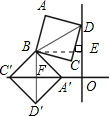
设BD=x,则A′C′=x,A′F=
x,
∵BD′⊥OC′,OD⊥OC′,
∴BD′∥OD,
∴∠BDO=180°-∠DBD′=180°-120°=60°,
∴OF=BE=BD•sin∠BDO=
x.
即
x+(
-1)=
x,
解得:x=2,
∴边长是:
x=
.
故答案是:
.

设BD=x,则A′C′=x,A′F=
| 1 |
| 2 |
∵BD′⊥OC′,OD⊥OC′,
∴BD′∥OD,
∴∠BDO=180°-∠DBD′=180°-120°=60°,
∴OF=BE=BD•sin∠BDO=
| ||
| 2 |
即
| 1 |
| 2 |
| 3 |
| ||
| 2 |
解得:x=2,
∴边长是:
| ||
| 2 |
| 2 |
故答案是:
| 2 |

练习册系列答案
相关题目